题目内容
【题目】在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．
（1）用树状图或列表法列举点M所有可能的坐标；
（2）求点M（x，y）在函数y＝﹣x+1的图象上的概率．
【答案】（1）列表见解析；共有9种等可能的结果数；（2）点M（x，y）在函数y＝﹣x+1的图象上的概率＝
．
【解析】
（1）通过列表展示所有9种等可能的结果数；（2）找出满足点（x，y）落在函数y=-x+1的图象上的结果数，然后根据概率公式求解.
解：（1）列表如下：
x y | 0 | 1 | 2 |
﹣1 | （0，﹣1） | （1，﹣1） | （2，﹣1） |
﹣2 | （0，﹣2） | （1，﹣2） | （2，﹣2） |
0 | （0，0） | （1，0） | （2，0） |
共有9种等可能的结果数；
（2）满足点（x，y）落在函数y＝﹣x+1的图象上的结果有2个，即（2，﹣1），（ 1，0 ），
所以点M（x，y）在函数y＝﹣x+1的图象上的概率＝．
天天向上一本好卷系列答案
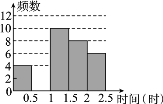
小学生10分钟应用题系列答案【题目】某中学对本校初中学生完成家庭作业的时间做了总量控制，规定学生每天完成家庭作业的时间少于1.5小时．该校数学课外兴趣小组对本校初中学生回家完成作业的时间作了一次随机抽样调查，并绘制出频数分布表和频数分布直方图的一部分．
时间(时) | 频数 | 频率 |
0≤t＜0.5 | 4 | 0.1 |
0.5≤t＜1 | a | 0.3 |
1≤t＜1.5 | 10 | 0.25 |
1.5≤t＜2 | 8 | b |
2≤t＜2.5 | 6 | 0.15 |
合计 | 1 |
(1)在频数分布表中，a＝________，b＝________；
(2)补全频数分布直方图；
(3)请估计该校1400名初中学生中，有多少名学生在1.5小时以内(不包括1.5小时)完成了家庭作业？
