题目内容
【题目】综合与实践：
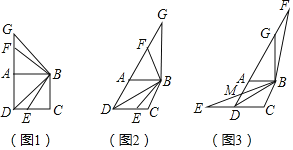
问题情境：（1）如图1，点E是正方形ABCD边CD上的一点，连接BD、BE，将∠DBE绕点B顺针旋转90°，旋转后角的两边分别与射线DA交于点F和点G．
①线段BE和BF的数量关系是 ；
②写出线段DE、DF和BD之间的数量关系，并说明理由；
操作探究：（2）在菱形ABCD中，∠ADC＝60°，点E是菱形ABCD边CD所在直线上的一点，连接BD、BE，将∠DBE绕点B顺时针旋转120°，旋转后角的两边分别与射线DA交于点F和点G．
①如图2，点E在线段DC上时，请探究线段DE、DF和BD之间的数量关系，写出结论并给出证明．
②如图3，点E在线段CD的延长线上时，BE交射线DA于点M，若DE＝DC＝2a，直接写出线段FM和AG的长度．
【答案】（1）①BE＝BF，见解析；②DF+DE＝
BD，理由见解析；（2）①DF+DE＝
BD，理由见解析；②FM＝7a，AG＝4a．
【解析】
（1）①根据旋转的性质解答即可；
②根据正方形的性质和全等三角形的判定和性质解答即可；
（2）①根据菱形的性质和全等三角形的判定和性质解答即可；
②根据相似三角形的判定和性质解答即可．
（1）①∵∠DBE绕点B顺针旋转90°，如图（1）
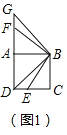
由旋转可知，∠DBE＝∠GBF，
∵四边形ABCD是正方形，
∴∠BDC＝∠ADB＝45°，
∵∠DBG＝90°，
∴∠G＝45°，
∴∠G＝∠BDG，
∴GB＝BD，
∴△GBF≌△DBE（SAS），
∴BE＝BF；
故答案为：BE＝BF
②DF+DE＝BD，理由如下：
由旋转可知，∠DBE＝∠GBF，
∵四边形ABCD是正方形，
∴∠BDC＝∠ADB＝45°，
∵∠DBG＝90°，
∴∠G＝45°，
∴∠G＝∠BDG，
∴GB＝BD，
∴△GBF≌△DBE（SAS），
∴DE＝GF，
∴DF+DE＝DG，
∵DG＝BD，
即DE+DF＝BD；
（2）①DF+DE＝BD，
理由如下：在菱形ABCD中，∠ADB＝∠CDB＝
∠ADC＝
，
由旋转120°得∠EBF＝∠DBG＝120°，∠EBD＝∠FBG，
在△DBG中，∠G＝180°﹣120°﹣30°＝30°，
∴∠BDG＝∠G＝30°，
∴BD＝BG，
∴△EBD≌△FBG（ASA），
∴DE＝FG，
∴DE+DF＝DF+FG＝DG，
过点B作BM⊥DG于点M，如图（2）
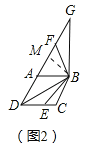
∵BD＝BG，
∴DG＝2DM，
在Rt△BMD中，∠BDM＝30°，
∴BD＝2BM．
设BM＝a，则BD＝2a，
，
∴DG＝2a，
，
∴DF+DE＝BD，
②过点B作BM⊥DG，BN⊥DC，如图（3）
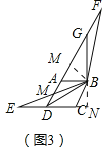
∵DE＝DC＝2a，
由①中同理可得：FM＝7a，AG＝4a．
