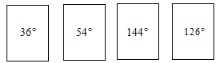
题目内容
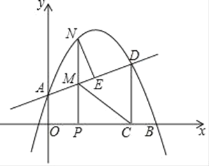
【题目】如图,已知锐角![]() 内接于⊙O,
内接于⊙O, ![]() 于点D,连结AO.
于点D,连结AO.
⑴若![]() .
.
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
⑵点E在线段OA上,![]() ,连接DE,设
,连接DE,设![]() ,
,![]() (m、n是正数),若
(m、n是正数),若![]() ,求证:
,求证:![]()

【答案】(1)①见解析;②△ABC面积的最大值是![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)①连接OB,OC,由圆的性质可得答案;
②先作AF⊥BC,垂足为点F,要使得面积最大,则当点A,O,D在同一直线上时取到
再根据三角形的面积公式即可得到答案;
(2)先设∠OED=∠ODE=α,∠COD=∠BOD=β,由锐角三角形性质得到
即![]() ,再结合题意及三角形内角和的性质得到
,再结合题意及三角形内角和的性质得到![]()
两式联立即可得到答案.
(1)①证明:连接OB,OC,
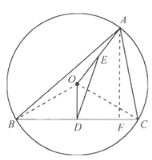
因为OB=OC,OD⊥BC,
所以∠BOD=![]() ∠BOC=
∠BOC=![]() ×2∠BAC=60°,
×2∠BAC=60°,
所以OD=![]() OB=
OB=![]() OA
OA
②作AF⊥BC,垂足为点F,
所以AF≤AD≤AO+OD=![]() ,等号当点A,O,D在同一直线上时取到
,等号当点A,O,D在同一直线上时取到
由①知,BC=2BD=![]() ,
,
所以△ABC的面积![]()
即△ABC面积的最大值是![]()
(2)设∠OED=∠ODE=α,∠COD=∠BOD=β,
因为△ABC是锐角三角形,
所以∠AOC+∠AOB+2∠BOD=360°,
即![]() (*)
(*)
又因为∠ABC<∠ACB,
所以∠EOD=∠AOC+∠DOC
![]()
因为∠OED+∠ODE+∠EOD=180°,
所以![]() (**)
(**)
由(*),(**),得![]() ,
,
即![]()

【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
|
|
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 |
| 2800 |
|
精加工获利/元 |
| 25800 |
|
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?