题目内容
【题目】如图,已知直线![]() 与抛物线
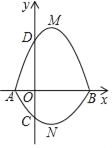
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
【答案】解:(1)把A(1,-4)代入![]() ,得k=2,∴
,得k=2,∴![]() 。
。
令y=0,解得:x=3,∴B的坐标是(3,0)。
∵A为顶点,∴设抛物线的解析为![]() 。
。
把B(3,0)代入得:4a-4=0,解得a=1。
∴抛物线的解析式为![]() 即
即![]() 。
。
(2)存在。
∵OB=OC=3,OP=OP,∴当∠POB=∠POC时,△POB≌△POC。
此时PO平分第二象限,即PO的解析式为y=-x。
设P(m,-m),则![]() ,解得
,解得![]() (
(![]() ,舍去)。
,舍去)。
∴P(![]() 。
。
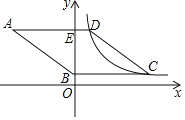
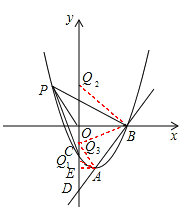
(3)①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() ,即
,即![]() 。
。
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴![]() ,即
,即![]() 。
。
∴![]() ,即
,即![]() 。
。
③如图,当∠AQ3B=90°时,作AE⊥y轴于E,则△BOQ3∽△Q3EA,
∴![]() ,即
,即![]() 。
。
∴![]() ,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
综上,Q点坐标为![]() 或
或![]() 或(0,-1)或(0,-3)。
或(0,-1)或(0,-3)。
【解析】
试题(1)已知点A坐标可确定直线AB的解析式,进一步能求出点B的坐标.点A是抛物线的顶点,那么可以将抛物线的解析式设为顶点式,再代入点B的坐标,依据待定系数法可解。
(2)首先由抛物线的解析式求出点C的坐标,在△POB和△POC中,已知的条件是公共边OP,若OB与OC不相等,那么这两个三角形不能构成全等三角形;若OB等于OC,那么还要满足的条件为:∠POC=∠POB,各自去掉一个直角后容易发现,点P正好在第二象限的角平分线上,联立直线y=-x与抛物线的解析式,直接求交点坐标即可,同时还要注意点P在第二象限的限定条件。
(3)分别以A、B、Q为直角顶点,分类进行讨论,找出相关的相似三角形,依据对应线段成比例进行求解即可。

 小题狂做系列答案
小题狂做系列答案