题目内容
【题目】 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
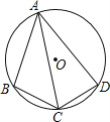
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求![]() 的值.
的值.
(3)若以点C为顶点的抛物线y=mx2-4mx-12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n-![]() ≤-
≤-![]() my02-40
my02-40![]() y0+298成立,求实数n的最大值.
y0+298成立,求实数n的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() ;(3)10+
;(3)10+![]() .
.
【解析】
(1)先由三角形两边之和大于第三边、两边之差小于第三边,求出AC长度的范围.因为三角形三边都有可能是平方等于另两边乘积的边,故需分三种情况讨论,计算并判断结果是否合理.
(2)①由BD平分∠ABC和AD∥BC可证得∠ABD=∠DBC=∠ADB,进而得AB=AD.因为BC为圆的直径,根据圆周角定理得∠BAC=∠CDA=90°,再加上平行所得的∠ACB=∠DAC,即证得△ABC∽△DCA,由对应边成比例得AC2=BCDA=BCAB,得证.
②由Rt△ABC、Rt△ACD、Rt△BCD根据勾股定理得BD2=BC2+CD2=AB2+AC2+AC2-AB2=2AC2,故有BD=![]() AC,进而得
AC,进而得![]() .
.
(3)先由抛物线解析式求点A、B、C坐标,求得AB=8,根据抛物线对称性有AC=BC.由△ABC是比例三角形可得AB2=BCAC或AC2=ABBC,化简后都得到AC=AB,把含m的式子代入即求得m的值,进而求得抛物线解析式和最大值.由于点M(x0,y0)在抛物线上,则得到y0的最大值.设z=-![]() my02-40
my02-40![]() y0+298,把m的值代入并配方,得到关于y0的二次函数关系,且对应抛物线开口向下.由于y0范围取不到此二次函数的顶点,故取y0的最大值求得z的最小值,进而得到n的最大值.
y0+298,把m的值代入并配方,得到关于y0的二次函数关系,且对应抛物线开口向下.由于y0范围取不到此二次函数的顶点,故取y0的最大值求得z的最小值,进而得到n的最大值.
(1)∵AB=2,BC=3,
∴1<AC<5,
①若AB2=BCAC,则AC=![]() ,
,
②若BC2=ABAC,则AC=![]() ,
,
③若AC2=ABBC=6,则AC=![]() ,
,
综上所述,满足条件的AC的长为![]() ,
,![]() ,
,![]() .
.
(2)①证明:∵AD∥BC,
∴∠DAC=∠ACB,∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∵点A在以BC为直径的圆上,
p>∴∠BAC=90°,∵∠BAC=∠CDA=90°,∠ACB=∠DAC,
∴△ABC∽△DCA,
∴![]() ,
,
∴AC2=BCDA=BCAB,
∴△ABC为比例三角形,
②∵∠BAC=∠CDA=90°,AB=AD,
∴BC2=AB2+AC2,AC2=AD2+CD2=AB2+CD2,
∵AD∥BC,
∴∠BCD=180°-∠ADC=90°,
∴BD2=BC2+CD2=AB2+AC2+AC2-AB2=2AC2,
∴BD=![]() AC,
AC,
∴![]() ;
;
(3)∵y=mx2-4mx-12m=m(x-2)2-16m(m<0),
∴抛物线开口向下,顶点C(2,-16m),
∵y=0时,mx2-4mx-12m=0,
解得:x1=-2,x2=6,
∴A(-2,0),B(6,0),AB=8,
∴AC=BC=![]() ,
,
∵△ABC是比例三角形,
∴AB2=BCAC或AC2=ABBC,
∴AB=AC,
∴4![]() =8,
=8,
解得:m1=![]() (舍去),m2=-
(舍去),m2=-![]() ,
,
∴抛物线解析式为y=-![]() x2+
x2+![]() x+3
x+3![]() =-
=-![]() (x-2)2+4
(x-2)2+4![]() ,
,
∵M(x0,y0)在抛物线上,
∴y0≤4![]() ,
,
设z=-![]() my02-40
my02-40![]() y0+298=4y02-40
y0+298=4y02-40![]() y0+298=4(y0-5
y0+298=4(y0-5![]() )2-2,
)2-2,
∴当y0≤4![]() 时,z随x的增大而减小,
时,z随x的增大而减小,
∴y0=4![]() 时,z最小值=4×(4
时,z最小值=4×(4![]() -5
-5![]() )2-2=4×3-2=10,
)2-2=4×3-2=10,
∵n-![]() ≤z恒成立,即n-
≤z恒成立,即n-![]() ≤10,
≤10,
∴n的最大值为10+![]() .
.

 名校课堂系列答案
名校课堂系列答案