题目内容
【题目】已知:![]() 是
是![]() 的角平分线,点
的角平分线,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]()
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() 为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
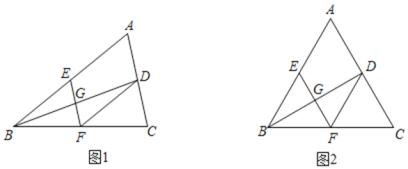
【答案】(1)详见解析;(2)△ABD≌△CBD,△BEF≌△FDC,△BGF≌△BGE,△BGE≌△DGF,△BGF≌△DGF
【解析】
(1)根据角平分线的性质及平行线的性质得到DF=BF,利用![]() ,
,![]() 即可求得结论;
即可求得结论;
(2)根据角平分线的性质即可证得△ABD≌△CBD;利用(1)的平行四边形的性质证得△BEF≌△FDC,再利用角平分线的性质及平行线的性质证得△BGF≌△BGE,△BGE≌△DGF,得到△BGF≌△DGF.
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵DF∥AB,
∴∠ABD=∠FDB,
∴∠DBC=∠FDB,
∴DF=BF,
∵BF=AE,
∴DF=AE,
∵DF∥AE,
∴四边形AEFD为平行四边形;
(2)∵![]() 为等边三角形,
为等边三角形,
∴AB=BC=AC,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠ABD=∠CBD,
∵BD=BD,
∴△ABD≌△CBD;
由(1)知四边形AEFD为平行四边形,
∴EF∥AC,
∴∠BEF=∠A=∠C=∠BFE=60°,
∵![]() ,
,
∴∠DFC=∠B=60°
∴△BEF和△CDF都是等边三角形,
∵BF=DF,
∴△BEF≌△FDC;
∵![]() 是等边
是等边![]() 的角平分线,
的角平分线,
∴∠ABD=∠CBD=30°,
∵DF∥AB,
∴∠BDF=∠ABD=30°,
∵∠BEF=∠BFE=60°,
∴∠BGE=∠BGF=∠DGF=90°,
∵BG=BG,
∴△BGF≌△BGE,
∵GF=GF,
∴△BGE≌△DGF,
∴△BGF≌△DGF

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.