题目内容
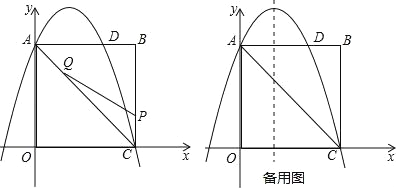
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+8;(2)①S=﹣
x+8;(2)①S=﹣![]() m2+3m;②满足条件的点F共有四个,坐标分别为F1(
m2+3m;②满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).
【解析】
(1)将A、C两点坐标代入抛物线y=-![]() x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
解:(1)将A、C两点坐标代入抛物线,得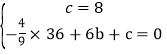 ,
,
解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8;
x+8;
(2)①∵OA=8,OC=6,
∴AC=![]() =10,
=10,
过点Q作QE⊥BC与E点,则sin∠ACB = ![]() =
= ![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QE=![]() (10﹣m),
(10﹣m),
∴S=![]() CPQE=
CPQE=![]() m
m![]() ×(10﹣m)=﹣
×(10﹣m)=﹣![]() m2+3m;
m2+3m;
②∵S=![]() CPQE=
CPQE=![]() m×
m×![]() (10﹣m)=﹣
(10﹣m)=﹣![]() m2+3m=﹣
m2+3m=﹣![]() (m﹣5)2+
(m﹣5)2+![]() ,
,
∴当m=5时,S取最大值;
在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8的对称轴为x=
x+8的对称轴为x=![]() ,
,
D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1(![]() ,8),
,8),
当∠FQD=90°时,则F2(![]() ,4),
,4),
当∠DFQ=90°时,设F(![]() ,n),
,n),
则FD2+FQ2=DQ2,
即![]() +(8﹣n)2+
+(8﹣n)2+![]() +(n﹣4)2=16,
+(n﹣4)2=16,
解得:n=6±![]() ,
,
∴F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ),
),
满足条件的点F共有四个,坐标分别为
F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).

 习题精选系列答案
习题精选系列答案【题目】近几年“雾霾”成为全社会关注的话题某校环保志愿者小组对该市2018年空气质量进行调查,从全年365天中随机抽查了50天的空气质量指数(AQI),得到以下数据:43、62、80、78、46、78、23、59、32、78、86、125、98、116、86、69、28、43、58、87、75、116、178、146、57、26、43、59、77、103、126、159、201、289、315、253、196、102、93、72、56、43、39、44、47、34、31、29、43、52.
(1)请你完成如下的统计表;
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 300以上 |
质量等级 | A(优) | B(良) | C(轻度污染) | D(中度污染) | E(重度污染) | F(严重污染) |
天数 |
(2)请你根据题中所给信息绘制该市2018年空气质量等级条形统计图;
(3)请你估计该市全年空气质量等级为“重度污染”和“严重污染”的天数.