题目内容
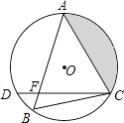
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.

【答案】1.5
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出∠CAF =∠DAF,由SAS证明△ADF≌△ACF,得出CF=DF,∠ADF=∠ACF=∠BDF=90°,设CF=DF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程即可.
连接DF,如图所示:

在Rt△ABC中,∠ACB=90°,AC=3,BC=4,由勾股定理求得AB=5,
∵AD=AC=3,AF⊥CD,
∴∠CAF =∠DAF,BD=AB-AD=2,
在△ADF和△ACF中,
∴△ADF≌△ACF(SAS),
∴∠ADF=∠ACF=90°,CF=DF,
∴∠BDF=90°,
设CF=DF=x,则BF=4-x,
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,
即x2+22=(4-x)2,
解得:x=1.5;
∴CF=1.5;
故答案为:1.5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目