Question

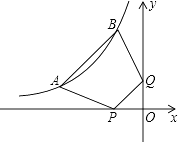
【题目】直线AB与⊙O相切于B点，C是⊙O与OA的交点，点D是⊙O上的动点（D与B，C不重合），若∠A=40°，则∠BDC的度数是（　　）
A.25°或155°
B.50°或155°
C.25°或130°
D.50°或130°

Answer 1

【答案】A
【解析】解：当点D在优弧BC上时，如图，
连结OB，
∵直线AB与⊙O相切于B点，
∴OB⊥BA，
∴∠OBA=90°，
∵∠A=40°，
∴∠AOB=50°，
∴∠BDC= ∠AOB=25°；
当点D在劣弧BC上时，即在D′点处，如图，
∵∠BDC+∠BD′C=180°，
∴∠BD′C=180°﹣25°=155°，
∴∠BDC的度数为25°或155°．
故选A．

【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．