题目内容
【题目】如图所示,在⊙O中, ![]() =
= ![]() ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 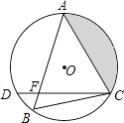
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
【答案】
(1)证明:∵ ![]() =
= ![]() ,
,
∴∠ACD=∠ABC,又∠BAC=∠CAF,
∴△ACF∽△ABC,
∴ ![]() =
= ![]() ,即AC2=ABAF;
,即AC2=ABAF;
(2)解:解:连接OA,OC,过O作OE⊥AC,垂足为点E,
如图所示:

∵∠ABC=60°,∴∠AOC=120°,
又∵OA=OC,∴∠AOE=∠COE= ![]() ×120°=60°,
×120°=60°,
在Rt△AOE中,OA=2cm,
∴OE=OAcos60°=1cm,
∴AE= ![]() =
= ![]() cm,
cm,
∴AC=2AE=2 ![]() cm,
cm,
则S阴影=S扇形OAC﹣S△AOC= ![]() ﹣
﹣ ![]() ×2
×2 ![]() ×1=(
×1=( ![]() ﹣
﹣ ![]() )cm2.
)cm2.
【解析】(1)由 ![]() =
= ![]() ,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;(2)连接OA,OC,利用同弧所对的圆心角等于圆周角的2倍,由∠B为60°,求出∠AOC为120°,过O作OE垂直于AC,垂足为点E,由OA=OC,利用三线合一得到OE为角平分线,可得出∠AOE为60°,在Rt△AOE中,由OA及cos60°的值,利用锐角三角函数定义求出OE的长,在Rt△AOE中,利用勾股定理求出AE的长,进而求出AC的长,由扇形AOC的面积﹣△AOC的面积表示出阴影部分的面积,利用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;(2)连接OA,OC,利用同弧所对的圆心角等于圆周角的2倍,由∠B为60°,求出∠AOC为120°,过O作OE垂直于AC,垂足为点E,由OA=OC,利用三线合一得到OE为角平分线,可得出∠AOE为60°,在Rt△AOE中,由OA及cos60°的值,利用锐角三角函数定义求出OE的长,在Rt△AOE中,利用勾股定理求出AE的长,进而求出AC的长,由扇形AOC的面积﹣△AOC的面积表示出阴影部分的面积,利用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
【考点精析】掌握圆心角、弧、弦的关系和圆周角定理是解答本题的根本,需要知道在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

【题目】某校九年级为建立学习兴趣小组,对语文、数学、英语、物理、化学、思想品德、历史、综合共八个科目的喜欢情况进行问卷调查(每人只选一项),下表是随机抽取部分学生的问卷进行统计的结果:
科目 | 语文 | 数学 | 英语 | 物理 | 化学 | 思想品德 | 历史 | 综合 |
人数 | 6 | 10 | 11 | 12 | 10 | 9 | 8 | 14 |

根据表中信息,解答下列问题:
(1)本次随机抽查的学生共有人;
(2)本次随机抽查的学生中,喜欢科目的人数最多;
(3)根据上表中的数据补全条形统计图;
(4)如果该校九年级有600名学生,那么估计该校九年级喜欢综合科目的学生有多少人.




