题目内容
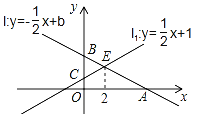
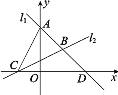
【题目】如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=![]() x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
【答案】(1) y=-x+4;(2)点B的坐标为(2,2);(3)6.
【解析】
(1)利用待定系数法即可求出直线l1的函数关系式为y=-x+4;
(2)解方程组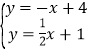 即可确定B点坐标;
即可确定B点坐标;
(3)求出点C坐标,根据S△ABC=S△ACD-S△BCD进行计算即可得.
(1)设直线l1的函数表达式为y=kx+b,
根据题意,得![]() ,解得:
,解得:![]() ,
,
所以直线l1的函数表达式为y=-x+4;
(2)根据题意,得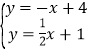 ,解得:
,解得:![]() ,
,
所以点B的坐标为(2,2);
(3)直线y=![]() x+1与x轴交于点C,所以点C坐标为(-2,0),
x+1与x轴交于点C,所以点C坐标为(-2,0),
所以CD=6,
所以,S△ABC=S△ACD-S△BCD=![]() =6.
=6.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
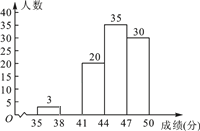
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?