题目内容
【题目】如图1,△ABC内接于圆,点D在劣弧![]() 上,AD=
上,AD=![]() BC,DC=
BC,DC=![]() AB,Q为AC中点,点D与点P关于点Q对称.
AB,Q为AC中点,点D与点P关于点Q对称.
(1)求证:△PAD∽△ABC.
(2)求证:点B,P,D在一条直线上.
(3)如图2,记∠PAB=α,∠PCB=β,∠ABC=θ,请用含α,β的代数式表示θ.
(4)如图3,设E,F分别为AB,BC的中点,EF交BD于点H,求![]() 的值.
的值.

【答案】(1)详见解析;(2)详见解析;(3)θ=90°﹣![]() ﹣
﹣![]() ;(4)
;(4)![]()
【解析】
(1)由对角线互相平分的四边形是平行四边形可证四边形APCD是平行四边形,可得AP=CD,AP∥CD,可证∠PAD=∠B,即可证△PAD∽△ABC;
(2)由相似三角形的性质可得∠ACB=∠ADP,又由∠ACB=∠ADB,可得∠ADP=∠ADB,可证点B,P,D在一条直线上;
(3)由外角性质可得∠APD+∠CPD=∠ABP+∠BAP+∠CBP+∠PCB=α+β+θ,由平行四边形的性质和圆的内接四边形的性质可得180°﹣∠ABC=α+β+θ,即可求解;
(4)根据题意连接EP,FP,由角的数量关系可求∠EPF=90°,通过相似三角形的判定和性质可证EH=HF,由直角三角形的性质可求PH=![]() EF=
EF=![]() AC,即可求解.
AC,即可求解.
解:(1)∵点Q为AC中点,点D与点P关于点Q对称,
∴AQ=QC,PQ=QD,
∴四边形APCD是平行四边形,
∴AP=CD,AP∥CD,
∴∠PAD+∠ADC=180°,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠PAD=∠B,
又∵![]() ,
,
∴△PAD∽△ABC.
(2)连接BD,如图2,
∵△PAD∽△ABC,
∴∠ACB=∠ADP,
∵∠ACB=∠ADB,
∴∠ADP=∠ADB
∴点B,P,D在一条直线上.
(3)∵∠APD=∠ABP+∠BAP,∠CPD=∠CBP+∠PCB,
∴∠APD+∠CPD=∠ABP+∠BAP+∠CBP+∠PCB=α+β+θ,
∵四边形APCD是平行四边形,
∴∠ADC=∠APC=∠APD+∠CPD,
∴180°﹣∠ABC=α+β+θ,
∴2θ=180°﹣α﹣β,
∴θ=90°﹣![]() ﹣
﹣![]() .
.
(4)连接EP,FP,
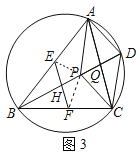
∵E,F分别为AB,BC的中点,
∴AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,
BC,
∵CD=![]() AB,CD=AP,
AB,CD=AP,
∴AE=AP,
∴∠APE=90°﹣![]() α,
α,
同理可得∠CPF=90°﹣![]() β,
β,
∴∠EPF=360°﹣∠APE﹣∠CPF﹣∠APC=180°﹣(![]() α+
α+![]() β+θ),
β+θ),
∵θ=90°﹣![]() ﹣
﹣![]() ,
,
∴∠EPF=180°﹣(![]() α+
α+![]() β+90°﹣
β+90°﹣![]() ﹣
﹣![]() )=90°,
)=90°,
∵E是AB的中点,点F是BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
∴△BEH∽△BAQ,△BFH∽△BCQ,
∴![]() ,
,
∵AQ=CQ,
∴EH=HF,
∴PH=![]() EF=
EF=![]() AC,
AC,
∴![]() .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案