题目内容
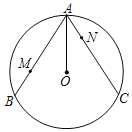
【题目】如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)过点O作OD⊥AB于点D,OE⊥AC于点E,利用角平分线的性质和垂径定理即可得出答案;
(2)联结OB,OM,ON,MN,首先证明![]() ,然后再证明
,然后再证明![]() ,根据相似三角形的性质即可得出答案.
,根据相似三角形的性质即可得出答案.
证明:(1)过点O作OD⊥AB于点D,OE⊥AC于点E,如图所示:
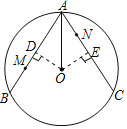
∵AO平分∠BAC.
∴OD=OE.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴AB=AC;
(2)联结OB,OM,ON,MN,如图所示,
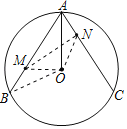
∵AM=CN,AB=AC
∴BM=AN.
∵OA=OB,
∴∠B=∠BAO.
∵∠BAO=∠OAN,
∴∠B=∠OAN,
∴△BOM≌△AON(SAS),
∴∠BOM=∠AON,OM=ON,
∴∠AOB=∠MON,
∴△NOM∽△BOA,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目