Question

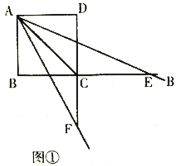
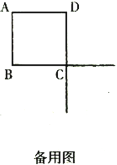
【题目】已知正方形ABCD的边长为8，一个以点A为顶点的45°角绕点A旋转，角的两边分别与边BC、DC的延长线交于点E、F，连接EF．设CE=a，CF=b．

（1）如图①，当a=8时，b的值为 ；

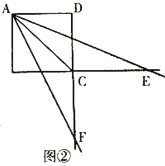
（2）如图②，当∠EAF被对角线AC平分时，求a、b的值；

（3）请写出∠EAF绕点A旋转的过程中a，b满足的关系式，并说明理由．

Answer 1

【答案】（1）16；（2）；（3），理由见解析

【解析】

（1）先判断出∠AFC+∠CAF=45°，判断出∠CAF=∠AEC，进而判断出△ACF∽△ECA，即可得出结论；

（2）先证明△ACF≌△ACE，从而得到CF=CE，然后再证明△ACE为等腰三角形，则CE=AC=8；

（3）先判断出∠AFC+∠CAF=45°，判断出∠CAF=∠AEC，进而判断出△ACF∽△ECA，即可得出结论．

（1）∵AC是正方形ABCD的对角线，

∴∠BCD=90°，∠ACB=45°，

∴∠ACF=135°，

∴∠AFC+∠CAF=45°，

∵∠AFC+∠AEC=180°-（∠CFE+∠CEF）-∠EAF=180°-90°-45°=45°，

∴∠CAF=∠AEC，

∵∠ACF=∠ACE=135°，

∴△ACF∽△ECA，

∴，

∴EC×CF=AC2=2AB2=128

∴ab=128，

∵a=8，

∴b=16；

（2）∵四边形是正方形，

∴

∵是正方形的对角线，

∴，∴，

∵被对角线平分，

∴，

在和中，，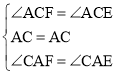

∴，∴，

∵，，

∴，

∵，

又∵，

∴，∴

在直角三角形中，

∴，即：．

（3）

理由：∵是正方形的对角线

∴，

∴

∵，

∴

∴

∴

∴

∵（已求）

，

∴