��Ŀ����
����Ŀ��ֱ��l��y=2x+2m(m>0)��x��y��ֱ���A.B���㣬��M��˫����![]() (x>0)��һ�㣬�ֱ�����MA��MB.
(x>0)��һ�㣬�ֱ�����MA��MB.
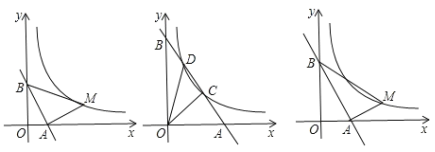
(1)��ͼ������A(![]() ��0)ʱ��ǡ��AB=AM����MAB=90��������M�����ꣻ
��0)ʱ��ǡ��AB=AM����MAB=90��������M�����ꣻ
(2)��ͼ����m=3ʱ��ֱ��l��˫���߽���C.D���㣬�ֱ�����OC��OD��������OCD�����
(3)��ͼ����˫�������Ƿ���ڵ�M��ʹ����ABΪֱ�DZߵ���MAB����AOB����?������ڣ���ֱ��д����M�����ꣻ��������ڣ���˵������.
���𰸡���1����![]() ��
��![]() ������2��3����3����4��1������2��2������
������2��3����3����4��1������2��2������![]() ��
��![]() ������
������![]() ��
��![]() ��.
��.
��������
��1����A���������ֱ�ߵĽ���ʽ�������m��ֵ��Ȼ��֤����OAB�ա�EMA�����ME��AE�ij�����M�����꼴����⣻
��2����һ�κ����뷴���������Ľ���ʽ��ɵķ����飬�������C��D�����꣬��DF��y���ڵ�F��CG��y�ᣬ����S��OCD=S����CDFG+S��OCG-S��ODF��⣻
��3���������ۣ��ԡ�BAM�͡�ABMΪֱ������������ٵ���BAM=��BOA=90��ʱ����MH��x���ڵ�H�������AM�ij����ٸ������������ε��������AH��MH�ij����������M�����꣬���뷴����������ϵʽ���m���ɣ��ڵ���ABM=90��ʱ������M��MH��y���ڵ�H��ͬ�������M����.
(1)��A(![]() ��0)����y=2x+2m�ã�
��0)����y=2x+2m�ã�![]() +2m=0��
+2m=0��
��ã�m=![]() .
.
��ֱ�ߵĽ���ʽ�ǣ�y=2x+![]() ��
��
��x=0,���y=![]() ��
��
��B��������(0, ![]() ).
).
��ͼ��ʾ����ME��x���ڵ�E.
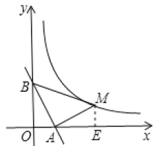
�ߡ�BAM=90�㣬
���BAO+��MAE=90�㣬
�֡�ֱ�ǡ�AEM��,��AME+��MAE=90�㣬
���BAO=��AME.
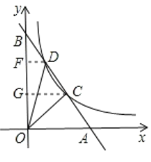
�ڡ�OAB�͡�EMA�У�
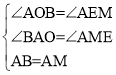
���OAB�ա�EMA(AAS)��
��ME=OA=![]() ,AE=OB=
,AE=OB=![]() .
.
��OE=OA+AE=![]() ��
��
��M��������(![]() ��
��![]() )��
)��
(2)��m=3ʱ��һ�κ����Ľ���ʽ��y=2x+6.
�ⲻ��ʽ��![]() ��
��
��![]() ��
��![]() ��
��
��D��������(1,4),C��������(2,2).
��ͼ����DF��y���ڵ�F��CG��y��,��F��G������ֱ���(0,4)��(0,2).
��S��OCG=S��ODF=![]() ��4=2��
��4=2��
S����CDFG=![]() ��(1+2)��(42)=3��
��(1+2)��(42)=3��
��S��OCD=S����CDFG+S��OCGS��ODF=3;
(3)��ͼ����MH��x���ڵ�H.
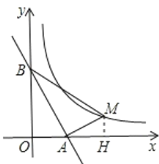
���AOB����ABM����AMH������ֱ�DZߵı���1:2��ֱ��������.
�ٵ���BAM=��BOA=90��ʱ��OA=m��OB=2m���ã�
AM=![]() AB=
AB=![]() m��MH=
m��MH=![]() OA=
OA=![]() ��
��
�Ӷ��õ���M������Ϊ(2m, ![]() ).
).
����˫���߽���ʽΪ��![]() =
=![]() ��
��
��ã�m=2,���M������Ϊ(4,1)��
ͬ������BAM=��OBAʱ,����õ�M������Ϊ(![]() ��
��![]() ).
).
�ڵ���ABM=90��ʱ������M��MH��y���ڵ�H��
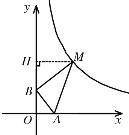
���AOB����ABM����BMH����ֱ�DZߵı���1:2��ֱ�������Σ�
����AMB=��OABʱ��OB=m��OA=2m��
�ã�AH=2OB=2m��MH=2OA=4m��
�Ӷ���M������Ϊ(4m,4m)
����˫���ߵĽ���ʽ�ã�4m��4m=4��
��ã�m=![]() ,��M������Ϊ(2,2)��
,��M������Ϊ(2,2)��
ͬ��,����AMB=��OBAʱ,��M������Ϊ(![]() ,
,![]() ).
).
�������������������ĵ�M�������ǣ���4��1������2��2������![]() ��
��![]() ������
������![]() ��
��![]() ��.
��.

����Ŀ����֪���κ���y��ax2��bx+c��y��x�IJ��ֶ���ֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��3 | 1 | 3 | 1 |
���н��ۢ������ߵĿ������£�����ͼ��ĶԳ���Ϊx��1���۵�x��1ʱ������ֵy��x����������ܷ���ax2+bx+c��0��һ��������4��������ȷ�Ľ�����_____