题目内容
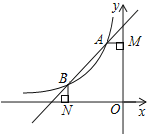
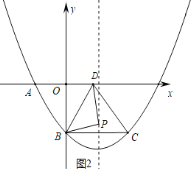
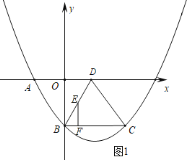
【题目】如图所示，菱形ABCD位于平面直角坐标系中，抛物线y＝ax2+bx+c经过菱形的三个顶点A、B、C，已知A（﹣3，0）、B（0，﹣4）．
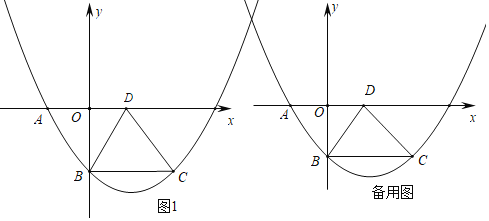
（1）求抛物线解析式；
（2）线段BD上有一动点E，过点E作y轴的平行线，交BC于点F，若S△BOD＝4S△EBF，求点E的坐标；
（3）抛物线的对称轴上是否存在点P，使△BPD是以BD为斜边的直角三角形？如果存在，求出点P的坐标；如果不存在，说明理由．
【答案】（1）
；（2）点E的坐标为（1，﹣2）；（3）存在，P的坐标为
或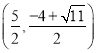
.
【解析】
（1）由点A，B的坐标可得出AB的长度，利用菱形的性质结合点B的坐标可得出点C的坐标，再由点A，B，C的坐标，利用待定系数法即可求出抛物线解析式；
（2）由EF∥OB，AD∥BC可得出∠OBD＝∠FEB，∠ODB＝∠FBE，进而可得出△BOD∽△EFB，利用相似三角形的性质及S△BOD＝4S△EBF，可得出BF＝1，由点B，D的坐标，利用待定相似法可求出直线BD的解析式，再利用一次函数图象上点的坐标特征可求出点E的坐标；
（3）利用二次函数的性质可得出抛物线的对称轴为直线x＝
，设点P的坐标为（，m），结合点B，D的坐标可得出BD2，BP2，DP2的值，利用勾股定理可得出关于m的一元二次方程，解之即可得出结论．
解：（1）∵点A的坐标为（﹣3，0），点B的坐标为（0，﹣4），
∴OA＝3，OB＝4，
∴AB＝
＝5．
∵四边形ABCD为菱形，
∴AD∥BC，BC＝AB＝5，
∴点C的坐标为（5，﹣4）．
将A（﹣3，0），B（0，﹣4），C（5，﹣4）代入y＝ax2+bx+c，得：
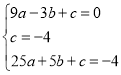，解得：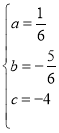
，
∴抛物线解析式为．
（2）∵EF∥OB，AD∥BC，
∴∠OBD＝∠FEB，∠ODB＝∠FBE，
∴△BOD∽△EFB，
∴
．
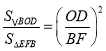∵S△BOD＝4S△EBF，
∴OD＝2BF．
∵AD＝AB＝5，OA＝3，
∴OD＝2，
∴点D的坐标为（2，0），BF＝1．
设直线BD的解析式为y＝kx+d（k≠0），
将B（0，﹣4），D（2，0）代入y＝kx+d，得：
，解得：
，
∴直线BD的解析式为y＝2x﹣4．
当x＝1时，y＝2x﹣4＝﹣2，
∴点E的坐标为（1，﹣2）．
（3）∵抛物线解析式为，
∴抛物线的对称轴为直线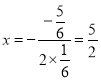
．
设点P的坐标为（，m），
∵点B的坐标为（0，﹣4），点D的坐标为（2，0），
∴BP2＝（﹣0）2+[m﹣（﹣4）]2＝m2+8m+
，
DP2＝（﹣2）2+（m﹣0）2＝m2+
，
BD2＝（2﹣0）2+[0﹣（﹣4）]2＝20．
∵△BPD是以BD为斜边的直角三角形，
∴BP2+DP2＝BD2，即m2+8m++m2+＝20，
整理，得：4m2+16m+5＝0，
解得：
， 
，
∴抛物线的对称轴上存在点P，使△BPD是以BD为斜边的直角三角形，点P的坐标为（，
）或（，
）．
