题目内容
【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
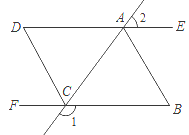
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
【答案】(1)平行,见解析;(2)平行,见解析;(3)平分,见解析.
【解析】
(1)依据∠CAE+∠2=180°,∠1+∠2=180°,即可得到∠1=∠CAE,进而判定DE∥BF;
(2)依据DE∥BF,可得∠B=∠EAB,进而得出∠D=∠EAB,进而判定AB∥CD;
(3)依据CD平分∠ACF,可得∠FCD=∠DCA,再根据平行线的性质,即可得到∠FCD=∠D=∠EAB,∠DCA=∠CAB,进而得出∠CAB=∠EAB,即AB平分∠CAE.
解: (1)平行,
因为∠CAE+∠2=180°,
∠1+∠2=180°,
所以,∠1=∠CAE,
所以,DE∥BF;
(2)平行,
由(1)得DE∥BF,
所以,∠B=∠EAB,
因为∠B=∠D,
所以,∠EAB=∠D,
所以,AB∥CD;
(3)平分,
∵CD平分∠ACF,
∴∠FCD=∠DCA,
又∵DE∥BF,AB∥CD,
∴∠FCD=∠D=∠EAB,∠DCA=∠CAB,
∴∠CAB=∠EAB,
即AB平分∠CAE.
故答案为:(1)平行,见解析;(2)平行,见解析;(3)平分,见解析.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目