题目内容
【题目】已知![]() ,OC平分∠AOB,点P是射线OC上的一点.
,OC平分∠AOB,点P是射线OC上的一点.

(1)如图一,过点P作PD⊥OA,PE⊥OB,说明PD与PE相等的理由.
(2)如图二,如果点F、G分别在射线OA、OB上,且∠FPG=60°,那么线段PF与PG相等吗?请说明理由;
(3)在(2)的条件下,联合FG,![]() 是什么形状的三角形,请说明理由.
是什么形状的三角形,请说明理由.
【答案】见解析
【解析】
(1)先判断出∠AOC=∠BOC,进而利用AAS判断出△POD≌△POE,即可得出结论;
(2)同(1)方法得出PM=PN,进而利用SAS判断出△PMF≌△PNG,即可得出结论;
(3)利用顶角是60°的等腰三角形是等边三角形判断即可得出结论,
解:(1)∵OC是∠AOB的平分线,

在△POD和△POE中
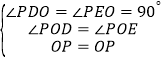
∴△POD≌△POE,
∴PD=PE;
(2)相等,理由:如图2,过点P作PM⊥OA于M,PN⊥OB于N,
![]()
同(1)的方法得,证得PM=PN
在四边形PMON,![]()

在△PMF和△PNG中

∴△PMF≌△PNG
∴PF=PG;
(3)△PFG是等边三角形
理由:如图2,连接FG,由(2)知,PF=PG,
∵∠FPG=60°,
∴△PFG是等边三角形,

练习册系列答案
相关题目
【题目】为了解某校学生的身高情况,王老师随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计图表:
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
身高情况分组表
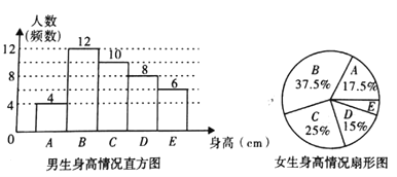
根据图表提供的信息,回答下列问题:
(1)样本中,女生身高在![]() 组的人数有_________人;
组的人数有_________人;
(2)在上面的扇形统计图中,表示![]() 组的扇形的圆心角是_________°;
组的扇形的圆心角是_________°;
(3)已知该校共有男生800人,女生760人,请估计该校身高在![]() 之间的学生约有多少人?
之间的学生约有多少人?