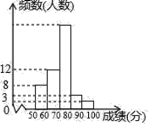题目内容
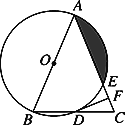
【题目】如图，已知△ABC：
（1）求作△ABC的内切圆⊙O，与边AB、BC、AC分别相切于点D、E、F；
（2）若AB=6，BC=8，AC=12，求AD、BE、CF的长度.
【答案】（1）见解析；（2）AD=5，BE=1，CF=7.
【解析】试题分析：（1）分别作∠BAC、∠ABC的角平分线交于点O，过点O作OD⊥AB，垂足为D，以O为圆心，以OD长为半径画圆即可得；
（2）设AD=x，由切线长定理可得AF=AD=x，BD=BE=6-x，CE=CF=12-x，列方程求解即可得.
试题解析： (1)如图所示；
(2)设AD=x，
则AF=AD=x，BD=BE=6-x，CE=CF=12-x，
依题意可列方程：(6-x)+(12-x)=8 ，
解方程得：x=5 ，
∴ BE=6-x=1，CF=12-x=7，
答：所求线段AD=5，BE=1，CF=7.
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
【题目】现有两个可以自由转动的转盘，每个转盘分成三个相同的扇形，涂色情况如图所示，指针的位置固定，同时转动两个转盘，回答以下问题：
圆1 圆2
圆2 圆1 | |||
(1)补全表格：圆1的所有可能结果有 种，分别是 ；
圆2的所有可能结果有 种，分别是 .
(2)写出：转盘停止后指针指向同种颜色区域的概率和至少有一指针指向红色区域的概率.
【题目】为了解某校学生的身高情况，王老师随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生人数相同，利用所得数据绘制如下统计图表：
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
身高情况分组表
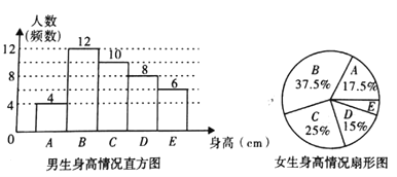
根据图表提供的信息，回答下列问题：
（1）样本中，女生身高在
组的人数有_________人；
（2）在上面的扇形统计图中，表示组的扇形的圆心角是_________°；
（3）已知该校共有男生800人，女生760人，请估计该校身高在
之间的学生约有多少人？
【题目】某中学1000名学生参加了“环保知识竞赛”，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：
成绩分组 | 频数 | 频率 |
50≤x＜60 | 8 | 0.16 |
60≤x＜70 | 12 | a |
70≤x＜80 | ■ | 0.5 |
80≤x＜90 | 3 | 0.06 |
90≤x＜90 | b | c |
合计 | ■ | 1 |
（1）写出
，
，
的值；
（2）请估计这1000名学生中有多少人的竞赛成绩不低于70分；
