题目内容
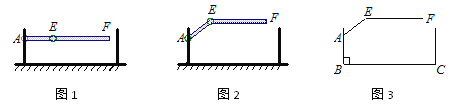
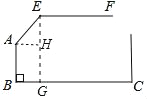
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
【答案】适合该地下车库的车辆限高标志牌为2.1米
【解析】试题分析:过点E作EG⊥BC于点G,AH⊥EG于点H,则∠AHE=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
试题解析:过点E作EG⊥BC于点G,AH⊥EG于点H.
∵EF∥BC,
∴∠GEF=∠BGE=90°
∵∠AEF=143°,
∴∠AEH=53°.
∴∠EAH=37°.
在△EAH中,AE=1.2,∠AHE=90°,
∴sin∠EAH="sin" 37°
∴![]()
∴EH=1.2×0.6=0.72.
∵AB⊥BC,
∴四边形ABGH为矩形.
∵GH=AB=1.2,
∴EG=EH+HG=1.2+0.72=1.92≈1.9.
答:适合该地下车库的车辆限高标志牌为1.9米.

练习册系列答案
相关题目