题目内容
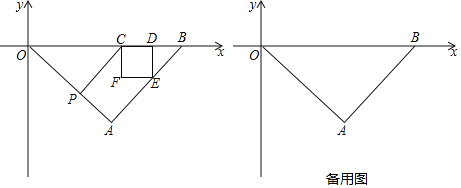
【题目】如图，平面直角坐标系中，点A在第四象限，点B在x轴正半轴上，在△OAB中，∠OAB＝90°，AB＝AO＝6
，点P为线段OA上一动点（点P不与点A和点O重合），过点P作OA的垂线交x轴于点C，以点C为正方形的一个顶点作正方形CDEF，使得点D在线段CB上，点E在线段AB上．
（1）①求直线AB的函数表达式．
②直接写出直线AO的函数表达式 ；
（2）连接PF，在Rt△CPF中，∠CFP＝90°时，请直接写出点P的坐标为 ；
（3）在（2）的前提下，直线DP交y轴于点H，交CF于点K，在直线OA上存在点Q．使得△OHQ的面积与△PKE的面积相等，请直接写出点Q的坐标 ．
【答案】（1）①y＝x﹣12；②y＝﹣x；（2）(3，﹣3)；（3）(2，﹣2)或(﹣2，2)
【解析】
（1）①利用等腰直角三角形的性质可以得到点A和点B的坐标，从而根据待定系数法求得直线AB的函数表达式；
②根据点A和点O的坐标可以求得直线AO的表达式；
（2）根据题意画出图形，首先得出点P、F、E三点共线，然后根据正方形的性质得出PE是△OAB的中位线，即点P为OA的中点，则点P的坐标可求；
（3）根据题意画出图形，然后求出直线PD 的解析式，得到点H的坐标，根据（2）中的条件和题意，可以求得△PKE的面积，再根据△OHQ的面积与△PKE的面积相等，可以得到点Q横坐标的绝对值，由点Q在直线AO上即可求得点Q的坐标．
解：（1）①∵在△OAB中，∠OAB＝90°，AB＝AO＝
，
∴△AOB是等腰直角三角形，OB＝
，
∴∠AOB＝∠ABO＝45°，
∴点A的坐标为（6，﹣6），点B的坐标为（12，0），
设直线AB的函数表达式为y＝kx+b，
，得
，
即直线AB的函数表达式是y＝x﹣12；
②设直线AO的函数表达式为y＝ax，
6a＝﹣6，得a＝﹣1，
即直线AO的函数表达式为y＝﹣x，
（2）点P的坐标为（3，﹣3），
理由：如图：
∵在Rt△CPF中，∠CFP＝90°，∠CFE＝90°，
∴点P、F、E三点共线，
∴PE∥OB，
∵四边形CDEF是正方形，∠OPC＝90°，∠COA＝45°，
∴CF＝PF＝AF＝EF，
∴PE是△OAB的中位线，
∴点P为OA的中点，
∴点P的坐标为（3，﹣3），
故答案为：（3，﹣3）；
（3）如图，
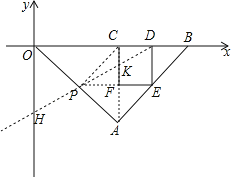
在△PFK和△DCK中，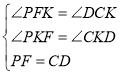
∴△PFK≌△DCK（AAS），
∴CK＝FK，
则由（2）可知，PE＝6，FK＝1.5，BD=3
∴点D（9，0）
∴△PKE的面积是
＝4.5，
∵△OHQ的面积与△PKE的面积相等，
∴△OHQ的面积是4.5，
设直线PD的函数解析式为y＝mx+n
∵点P（3，﹣3），点D（9，0）在直线PD上，
∴
，得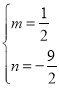
，
∴直线PD的函数解析式为y＝
，
当x＝0时，y＝-
，
即点H的坐标为
，
∴OH＝
设点Q的横坐标为q，
则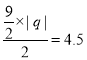
，
解得，q＝±2，
∵点Q在直线OA上，直线OA的表达式为y＝﹣x，
∴当x＝2时，y＝﹣2，当x＝﹣2时，x＝2，
即点Q的坐标为（2，﹣2）或（﹣2，2），
