题目内容
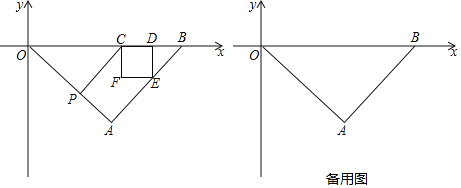
【题目】如图![]() ,已知直线
,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,以
两点,以![]() 为直角顶点在第二象限作等腰
为直角顶点在第二象限作等腰![]() .
.
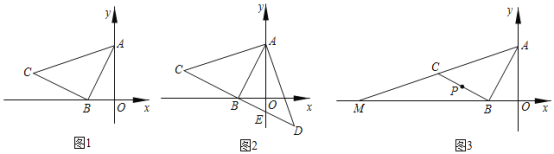
(1)求点![]() 的坐标,并求出直线
的坐标,并求出直线![]() 的关系式;
的关系式;
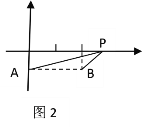
(2)如图![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,在直线
,在直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
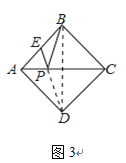
(3)如图![]() ,在(1)的条件下,直线
,在(1)的条件下,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点,在
上一点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 面积等于
面积等于![]() 面积的一半?若存在,请求出点
面积的一半?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+4;(2)见解析;(3)存在,点N(﹣
x+4;(2)见解析;(3)存在,点N(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)根据题意证明△CHB≌△BOA(AAS),即可求解;
(2)求出B、E、D的坐标分别为(-1,0)、(0,![]() )、(1,-1),即可求解;
)、(1,-1),即可求解;
(3)求出BC表达式,将点P代入,求出a值,再根据AC表达式求出M点坐标,由S△BMC=![]() MB×yC=
MB×yC=![]() ×10×2=10,S△BPN=
×10×2=10,S△BPN=![]() S△BCM=5=
S△BCM=5=![]() NB×a=
NB×a=![]() 可求解.
可求解.
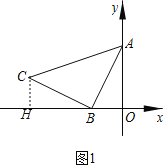
解:(1)令x=0,则y=4,令y=0,则x=﹣2,
则点A、B的坐标分别为:(0,4)、(﹣2,0),
过点C作CH⊥x轴于点H,
∵∠HCB+∠CBH=90°,∠CBH+∠ABO=90°,
∴∠ABO=∠BCH,
∠CHB=∠BOA=90°,BC=BA,
在△CHB和△BOA中,
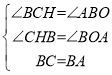 ,
,
∴△CHB≌△BOA(AAS),
∴BH=OA=4,CH=OB=2,
∴ 点C(﹣6,2),
将点A、C的坐标代入一次函数表达式:y= m x+ b得:![]() ,
,
解得: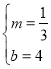 ,
,
故直线AC的表达式为:y=![]() x+4;
x+4;
(2)同理可得直线CD的表达式为:y=﹣![]() x﹣1①,则点E(0,﹣1),
x﹣1①,则点E(0,﹣1),
直线AD的表达式为:y=﹣3x+4②,
联立①②并解得:x=2,即点D(2,﹣2),
点B、E、D的坐标分别为(﹣
故点E是BD的中点,即BE=DE;
(3)将点BC的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣![]() x-1,
x-1,
将点P(﹣![]() ,a)代入直线BC的表达式得:
,a)代入直线BC的表达式得:![]() ,
,
直线AC的表达式为:y=![]() x+4,
x+4,
令y=0,则x=-12,则点M(﹣12,0),
S△BMC=![]() MB×y C=
MB×y C=![]() ×10×2=10,
×10×2=10,
S△BPN=![]() S△BCM=5=
S△BCM=5=![]() NB×a=
NB×a=![]() ,
,
解得:NB=![]() ,
,
故点N(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案