Question

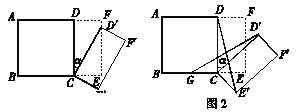
【题目】如图，△ABC是等边三角形，△ACE是等腰三角形，∠AEC＝120°，AE＝CE，F为BC中点，连接AE．

（1）直接写出∠BAE的度数为　 　；

（2）判断AF与CE的位置关系，并说明理由．

Answer 1

【答案】（1）90°；（2）AF∥EC，见解析

【解析】

（1）分别利用等边三角形的性质和等腰三角形的性质求出∠BAC，∠CAE的度数，然后利用∠BAE＝∠BAC+∠CAE即可解决问题；

（2）根据等边三角形的性质有AF⊥BC，然后利用等边三角形的性质和等腰三角形的性质得出，∠BCE＝90°则有EC⊥BC，再根据垂直于同一条直线的两直线平行即可得出结论．

解：（1）∵△ABC是等边三角形，

∴∠BAC＝∠ACB＝60°，

∵EA＝EC，∠AEC＝120°，

∴EAC＝∠ECA＝30°，

∴∠BAE＝∠BAC+∠CAE＝90°．

故答案为90°．

（2）结论：AF∥EC．

理由：∵AB＝AC，BF＝CF，

∴AF⊥BC，

∵∠ACB＝60°，∠ACE＝30°，

∴∠BCE＝90°，

∴EC⊥BC，

∴AF∥EC．