Question

【题目】在中，，，点是线段上一动点（不与，重合）.

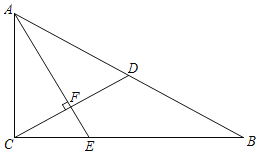
（1）如图1，当点为的中点，过点作交的延长线于点，求证：；

（2）连接，作，交于点.若时，如图2．

①______；

②求证：为等腰三角形；

（3）连接CD，∠CDE=30°，在点的运动过程中，的形状可以是等腰三角形吗？若可以，请求出的度数；若不可以，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）①120°；②证明见解析；（3）可以是等腰三角形，此时的度数为或．

【解析】

（1）先证明△ACD与△BFD全等，即可得出结论；

（2）①先根据等边对等角及三角形的内角和求出∠B的度数，再由平行线的性质可得出∠ADE的度数，最后根据平角的定义可求出∠CDB的度数；②根据等腰三角形的性质以及平行线的性质可得出∠A=∠EDA，从而可得出结论；

（3）先假设△ECD可以是等腰三角形，再分以下三种情况：I.当时，；II.当时，；III.当时，，然后再根据等腰三角形的性质、三角形的内角和以及三角形外角的性质求解即可．

（1）证明：，是的中线，

．

，．

，

，

；

（2）①解：∵AC=BC，∠ACB=120°，

∴∠A=∠B=（180°-120°）÷2=30°，

又DE∥BC，

∴∠ADE=∠B=30°，

∴∠CDB=180°-∠ADE-∠EDC=120°，

故答案为：；

②证明：，．

，．

，

为等腰三角形．

（3）解：可以是等腰三角形，理由如下：

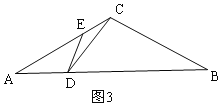
I.当时，，如图3，

．

，

．

II.当时，，如图4，

，

．

．

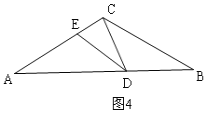
III.当时，．

∴，

，

此时，点与点重合，不合题意．

综上所述，可以是等腰三角形，此时的度数为或．