Question

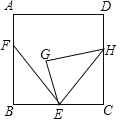
【题目】如图，正方形 ABCD 中，点 E，F 分别在 BC 和 AB 上，BE＝3，AF＝2，BF＝4，将△ BEF 绕点 E 顺时针旋转，得到△GEH，当点 H 落在 CD 边上时，F，H 两点之间的距离为_____．

Answer 1

【答案】6

【解析】

先确定正方形ABCD的边长AB＝6，则CE＝3，再利用勾股定理计算出EF＝5，根据旋转的性质得EF＝EH＝5，接着计算出CH＝4，从而可得到CH＝BF，于是可判定四边形BCHF为矩形，然后利用矩形的性质确定FH的长．

正方形ABCD的边长AB＝6,

而BE＝3，则CE＝3,

在Rt△BEF中，EF＝,

∵△BEF绕点E顺时针旋转，得到△GEH,

∴EF＝EH＝5,

在Rt△EHC中，CH＝,

∴CH＝BF＝4，

∴四边形BCHF为矩形，

∴FH＝BC＝6．

故答案为:6．