题目内容
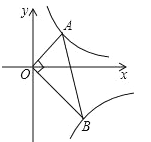
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
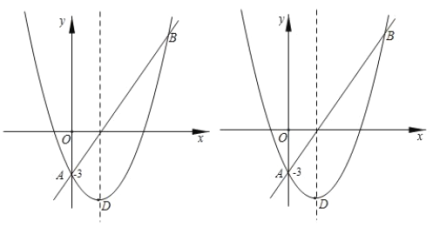
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
【答案】(1)![]() ,顶点D(2,
,顶点D(2,![]() );(2)C(
);(2)C(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0);(3)
,0);(3)![]()
【解析】
(1)抛物线的顶点D的横坐标是2,则x![]() 2,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入函数表达式,即可求解;
2,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入函数表达式,即可求解;
(2)分AB=AC、AB=BC、AC=BC,三种情况求解即可;
(3)由S△PAB![]() PHxB,即可求解.
PHxB,即可求解.
(1)抛物线的顶点D的横坐标是2,则x![]() 2①,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3②,联立①、②解得:a
2①,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3②,联立①、②解得:a![]() ,b
,b![]() ,c=﹣3,∴抛物线的解析式为:y
,c=﹣3,∴抛物线的解析式为:y![]() x2
x2![]() x﹣3.
x﹣3.
当x=2时,y![]() ,即顶点D的坐标为(2,
,即顶点D的坐标为(2,![]() );
);
(2)A(0,﹣3),B(5,9),则AB=13,设点C坐标(m,0),分三种情况讨论:
①当AB=AC时,则:(m)2+(﹣3)2=132,解得:m=±4![]() ,即点C坐标为:(4
,即点C坐标为:(4![]() ,0)或(﹣4
,0)或(﹣4![]() ,0);
,0);
②当AB=BC时,则:(5﹣m)2+92=132,解得:m=5![]() ,即:点C坐标为(5
,即:点C坐标为(5![]() ,0)或(5﹣2
,0)或(5﹣2![]() ,0);
,0);
③当AC=BC时,则:5﹣m)2+92=(m)2+(﹣3)2,解得:m=![]() ,则点C坐标为(
,则点C坐标为(![]() ,0).
,0).
综上所述:存在,点C的坐标为:(±4![]() ,0)或(5
,0)或(5![]() ,0)或(
,0)或(![]() ,0);
,0);
(3)过点P作y轴的平行线交AB于点H.设直线AB的表达式为y=kx﹣3,把点B坐标代入上式,9=5k﹣3,则k![]() ,故函数的表达式为:y
,故函数的表达式为:y![]() x﹣3,设点P坐标为(m,
x﹣3,设点P坐标为(m,![]() m2
m2![]() m﹣3),则点H坐标为(m,
m﹣3),则点H坐标为(m,![]() m﹣3),S△PAB
m﹣3),S△PAB![]() PHxB
PHxB![]() (
(![]() m2+12m)=-6m2+30m=
m2+12m)=-6m2+30m=![]() ,当m=
,当m=![]() 时,S△PAB取得最大值为:
时,S△PAB取得最大值为:![]() .
.
答:△PAB的面积最大值为![]() .
.