题目内容
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,AF是梯 形的 高,梯形面积是49cm2,则AF= ;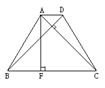

7
由等腰梯形的性质可得:BD=AC,
∴1/2BD2=49,
∴BD= ;
;
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,又∠BOC=90°,
∴∠OCB=45°,又AF⊥FC,
∴△AFC为等腰直角三角形,且斜边AC=DB= ,
,
根据勾股定理得:AF2+FC2=AC2,
∴2AF2=98,
解得AF=7.
∴1/2BD2=49,
∴BD=
 ;
;∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,又∠BOC=90°,
∴∠OCB=45°,又AF⊥FC,
∴△AFC为等腰直角三角形,且斜边AC=DB=
 ,
,根据勾股定理得:AF2+FC2=AC2,
∴2AF2=98,
解得AF=7.

练习册系列答案
相关题目
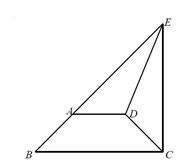
 中,
中, ∥
∥ ,
,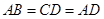 ,点
,点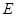 在
在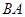 的延长线上,
的延长线上,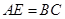 ,
,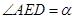 .
.
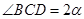 ;
;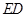 平分
平分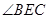 时,求证:△
时,求证:△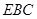 是等腰直角三角形.
是等腰直角三角形.



 ,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?
,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?