题目内容
如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD于E.
(1)求证:△APB∽△PEC;
(2)若CE=3,求BP的长.
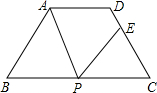
(1)求证:△APB∽△PEC;
(2)若CE=3,求BP的长.

(1)证明:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠B=∠C=60°,
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP,
∵∠APE=∠B,
∴∠BAP=∠EPC,
∴△APB∽△PEC;
 (2)过点A作AF∥CD交BC于点F,
(2)过点A作AF∥CD交BC于点F,
∵AD∥BC,
∴四边形ADCF是平行四边形,
∵∠AFB=∠C=∠B=60°,
∴△ABF为等边三角形,
∴CF=AD=3,AB=BF=7-3=4,
∵△APB∽△PEC,
∴
=
,
设BP=x,则PC=7-x,
∵EC=3,AB=4,
∴
=
,
解得:x1=3,x2=4,
经检验:x1=3,x2=4是原分式方程的解,
∴BP的长为:3或4.
∴∠B=∠C=60°,
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP,
∵∠APE=∠B,
∴∠BAP=∠EPC,
∴△APB∽△PEC;
 (2)过点A作AF∥CD交BC于点F,
(2)过点A作AF∥CD交BC于点F,∵AD∥BC,
∴四边形ADCF是平行四边形,
∵∠AFB=∠C=∠B=60°,
∴△ABF为等边三角形,
∴CF=AD=3,AB=BF=7-3=4,
∵△APB∽△PEC,
∴
| BP |
| EC |
| AB |
| PC |
设BP=x,则PC=7-x,
∵EC=3,AB=4,
∴
| x |
| 3 |
| 4 |
| 7-x |
解得:x1=3,x2=4,
经检验:x1=3,x2=4是原分式方程的解,
∴BP的长为:3或4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目