题目内容
【题目】阅读下面材料:
在数轴上2与﹣1所对的两点之间的距离:|2﹣(﹣1)|=3;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣3与﹣1所对的两点之间的距离:|(﹣1)﹣(﹣3)|=2
归纳:在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|或|b﹣a|

回答下列问题:
(1) 数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为: .
(3)继续请你在草稿纸上画出数轴,探究当x=_______时,|x-3|+|x+2|=7.
【答案】(1)|x-1|,-2;(2)5;(3)-3或4.
【解析】
(1)根据题意找出数轴上任意点间的距离的计算公式,然后进行计算即可;
(2)先化简绝对值,然后合并同类项即可;
(3)分为x>3和x<-2两种情况讨论.
(1)数轴上表示x和1的两点之间的距离=|x-1|;
数轴上表示数x和2的两点之间的距离表示为|x+2|;
(2)∵表示数x的点在﹣2与3之间移动,
∴2x3
当2x3时,|x-3|+|x+2|=3x + x+2=5;
(3)由(2)可知当2x3时,|x﹣3|+|x+2|的值总是一个固定的值5,不等于7;
所以可分两种情况:
当x>3时,x3+x+2=7,
解得:x=4;
当x<2时,3xx2=7.
解得x=3.
∴x=3或x=4.
故答案为:(1)|x-1|,-2;(2)5;(3)-3或4.

 阅读快车系列答案
阅读快车系列答案【题目】某学校开展“文明礼仪”演讲比赛,八(1)班、八(2)班派出的5名选手的比赛成绩如图所示.
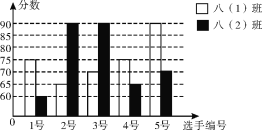
(1)根据上图,完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
(2)结合两班选手成绩的平均数和方差,分析两个班级参加比赛的选手的成绩.
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些?并说明理由.