��Ŀ����
����Ŀ����֪����������A��B���㣬��A��ʾ����Ϊ4����B��A�����ߣ���AB=12������һ����P�������ϵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶�������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������������˶������˶�ʱ��Ϊt�룮
![]()
(1)д�������ϵ�B��ʾ����Ϊ________��P����ʾ����Ϊ________(�ú�t�Ĵ���ʽ��ʾ)��
(2)����P��Q�ֱ��A��B����ͬʱ�������ʵ�P�˶���������Q���3����λ����?
(3)����P��Q�ֱ��A��B����ͬʱ�������ֱ���BQ��APΪ�ߣ��������Ϸ���������BQCD��������APEF��ͼ��ʾ.��tΪ��ֵʱ�����������ε��ص����������������APEF�����һ�룿��ֱ��д�����ۣ�t=__________��.

���𰸡�(1)-8��4-t��(2)3��5��(3)4.8��24.
��������
��1��������֪�ɵ�B���ʾ����Ϊ4-12����P��ʾ����Ϊ4-t��
��2�� ���P�˶�x��ʱ����Q���3����λ���ȣ������������P����Q���Ҳ࣬P����Q����࣬�ֱ��г����̼�����⣻
��3���ɷ������������ͼһ��P��Q���߶�AB�ϣ���ͼ����P��Q���߶�AB�⣬���������г�����t�ķ��̼������.
(1)�ߵ�A��ʾ����Ϊ4��B��A����ߣ�AB=12��
���B��ʾ������412=8��
�߶���P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶���
���P��ʾ������4t.
(2)���P�˶�x��ʱ����Q���3����λ���ȣ������������
![]()
P����Q���Ҳ�ʱ��
��AP=x��BQ=2x��
��AP+BQ=AB3��
��x+2x=9��
��ã�x=3��
![]()
P����Q�����ʱ��
��AP+BQ=AB+3��
��x+2x=15
��ã�x=5.
���P�˶�3���5��ʱ���Q���3����λ���ȡ�
(3) �����������
��ͼһ�� 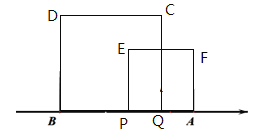
ͼһ
�����������ε��ص����������������APEF�����һ��,AP=t,BQ=2t,
��AQ=PQ=![]() ,
,
��2t+![]() =12 ���t=4.8
=12 ���t=4.8
��ͼ����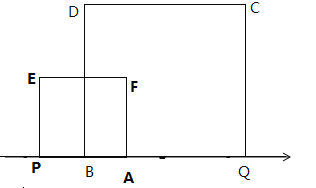
ͼ��
�����������ε��ص����������������APEF�����һ��,AP=t,BQ=2t,
��AB=PB=![]() ,
,
��![]() =12 ���t=24.
=12 ���t=24.
�ʴ�Ϊ��(1)-8��4-t��(2)3��5��(3)4.8��24.

 �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�






