题目内容
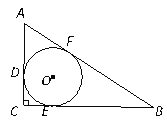
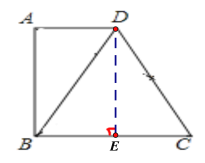
【题目】如图，在直角梯形ABCD中，
，
，
，联结BD，若△BDC是等边三角形，那么梯形ABCD的面积是_________；
【答案】
【解析】作DE⊥BC,先证四边形ABED是矩形，得AD=BE=3,AB=DE,再根据等边三角形性质得到BC=2BE=6,∠BDE=60°,再利用勾股定理可求得高，再运用梯形面积计算公式可求得结果.
作DE⊥BC,
因为四边形ABCD的直角梯形，
，
，
所以，四边形ABED是矩形，
所以，AD=BE=3,AB=DE,
又因为，三角形BCD是等边三角形，
所以，BC=2BE=6,∠BDE=60°,
所以，在直角三角形BED中，BD=BC=6,由勾股定理可得
DE=
,
所以，AB=DE=
所以，梯形ABCD的面积是：
故答案为：
练习册系列答案
相关题目
【题目】随着科技的发展，电动汽车的性能得到显著提高，某市对市场上电动汽车的性能进行随机抽样调查，现随机抽取部分电动汽车，记录其一次充电后行驶的里程数，并将抽查数据绘制成如下频数分布直方表和条形统计图．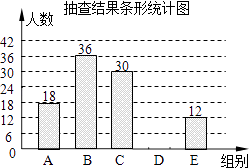 
根据以上信息回答下列问题：
组别 | 行驶里程x（千米） | 频数（台） | 频率 |
A | x＜200 | 18 | 0.15 |
B | 200≤x＜210 | 36 | a |
C | 210≤x＜220 | 30 | 0.25 |
D | 220≤x＜230 | b | 0.20 |
E | x≥230 | 12 | 0.10 |
根据以上信息回答下列问题：
（1）填空：a= ， b=；
（2）请将条形统计图补充完整；
（3）若该市市场上的电动汽车有2000台，请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数．
