题目内容
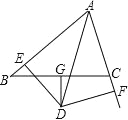
【题目】如图,![]() 中,
中,![]() ,D,E,F分别为AB,BC,CA上的点,且
,D,E,F分别为AB,BC,CA上的点,且![]() ,
,![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)证明见解析;(2)55°.
【解析】
(1)根据三角形外角的性质可得到∠CEF=∠BDE,可证△BDE≌△CEF;
(2)由(1)可得DE=FE,即△DEF是等腰三角形,由等腰三角形的性质可求出∠B=70°,即∠DEF=∠B=70°,从而求出∠EDF的度数.
(1)∵∠DEC=∠B+∠BDE=∠CEF+∠DEF,∠DEF=∠B,∴∠CEF=∠BDE.
∵AB=AC,∴∠C=∠B.
又∵CE=BD,∴△BDE≌△CEF.
(2)∵△BDE≌△CEF,∴DE=FE.
∴△DEF是等腰三角形,∴∠EDF=∠EFD.
∵AB=AC,∠A=40°,∴∠B=70°.
∵∠DEF=∠B,∴∠DEF=70°,∴∠EDF=∠EFD=![]() ×(180°﹣70°)=55°.
×(180°﹣70°)=55°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目