题目内容
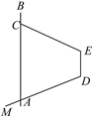
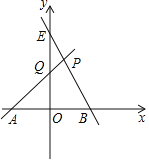
【题目】如图,已知直线AQ与x轴负半轴交于点A,与y轴正半轴交于点Q,∠QAO=45°,直线AQ在y轴上的截距为2,直线BE:y=-2x+8与直线AQ交于点P.
(1)求直线AQ的解析式;
(2)在y轴正半轴上取一点F,当四边形BPFO是梯形时,求点F的坐标.
(3)若点C在y轴负半轴上,点M在直线PA上,点N在直线PB上,是否存在以Q、C、M、N为顶点的四边形是菱形,若存在请求出点C的坐标;若不存在请说明理由.
【答案】(1)直线AQ的解析式为y=x+2;(2)F(0,4);(3)存在,C(0,![]() )或C(0,-10)
)或C(0,-10)
【解析】
(1)利用待定系数法即可求出直线AQ的解析式;
(2)先求出直线AQ和直线BE的交点P的坐标,由PF∥x轴可知F横坐标为0,纵坐标与点P的纵坐标相等;
(3)分CQ为菱形的对角线与CQ是菱形的一条边两种情况讨论.
解:(1)设直线AQ的解析式为y=kx+b,
∵直线AQ在y轴上的截距为2,
∴b=2,
∴直线AQ的解析式为y=kx+2,
∴OQ=2,
在Rt△AOQ中,∠OAQ=45°,
∴OA=OQ=2,
∴A(-2,0),
∴-2k+2=0,
∴k=1,
∴直线AQ的解析式为y=x+2;
(2)由(1)知,直线AQ的解析式为y=x+2①,
∵直线BE:y=-2x+8②,
联立①②解得![]() ,
,
∴P(2,4),
∵四边形BPFO是梯形,
∴PF∥x轴,
∴F(0,4);
(3)设C(0,c),
∵以Q、C、M、N为顶点的四边形是菱形,
①当CQ是对角线时,CQ与MN互相垂直平分,
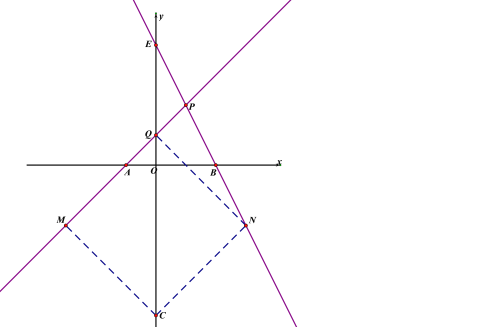
设C(0,c),
∵CQ的中点坐标为(0,![]() ),
),
∴点M,N的纵坐标都是![]() ,
,
∴M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
∴![]() +
+![]() =0,
=0,
∴c=-10,
∴C(0,-10),
②当CQ为边时,CQ∥MN,CQ=MN=QM,
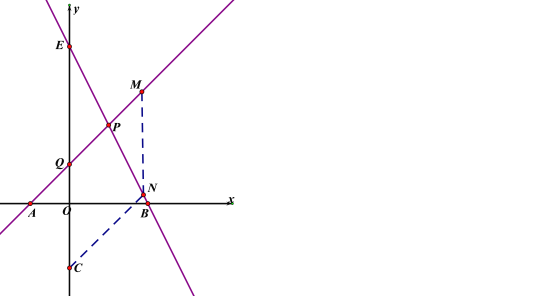
设M(m,m+2),
∴N(m,-2m+8),
∴|3m-6|=2-c=![]() |m|,
|m|,
∴m=![]() 或m=
或m=![]() ,
,
∴c=![]() 或c=
或c=![]() (舍),
(舍),
∴![]() ,
,
∴(0,![]() )或C(0,-10).
)或C(0,-10).

 阅读快车系列答案
阅读快车系列答案