题目内容
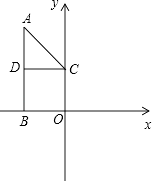
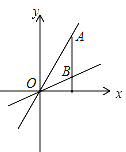
【题目】在△AOB中，∠AOB=90°，AO=6厘米，BO=8厘米，分别以OB和OA所在直线为x轴，y轴建立平面直角坐标系，如图所示，动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动，同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动（其中一点到达终点时，另一点随即停止移动）．
（1）求过点A和点B的直线表达式；
（2）当点M移动多长时间时，四边形AMNB的面积最小？并求出四边形AMNB面积的最小值；
（3）在点M和点N移动的过程中，是否存在以O，M，N为顶点的三角形与△AOB相似？若存在，请求出点M 和点N的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵AO=6厘米，BO=8厘米，
∴A（0，6），B（8，0）．
设AB的解析式为y=kx+b，由题意，得
，
解得：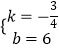 
，
∴直线AB的解析式为y=﹣ 
x+6；
（2）
解：设四边形AMNB的面积为S，M、N运动的时间为t，由题意，得
AM=2t，ON=4t，
∴OM=6﹣2t，
∴S△OMN= 
（6﹣2t）4t=﹣4t2+12t．
∴S= 
﹣（﹣4t2+12t），
=24+4t2﹣12t，
=4（t﹣ 
）2+15．
∵a=4＞0，
∴抛物线的开口向上，
∴当t= 时，S最小=15．
答：当点M移动 秒时，四边形AMNB的面积最小，最小值为15厘米2；
（3）
解：当△OMN∽△OAB时，
∴ 
，
∴ 
，
∴t= 
．
∴OM=6﹣2× = 
，ON=4× = 
，
∴M（0， ），N（ ，0）；
当△ONM∽△OAB时，
∴ 
，
∴ 
，
∴t= 
．
∴OM=6﹣2× = 
，ON=4× = 
，
∴M（0， ），N（ 
，0）
【解析】（1）根据条件可以求出点A和点B的坐标，然后运用待定系数法就可以求出解析式；（2）设四边形AMNB的面积为S，M、N运动的时间为t，表示出S与t的函数关系式，再由其解析式就可以求出结论；（3）分类讨论，当△OMN∽△OAB和△ONM∽△OAB时分别求出t的值就可以求出M、N的坐标．
【考点精析】利用确定一次函数的表达式和相似三角形的性质对题目进行判断即可得到答案，需要熟知确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；对应角相等，对应边成比例的两个三角形叫做相似三角形．
