Question

【题目】已知抛物线的顶点为（0，4）且与x轴交于（﹣2，0），（2，0）．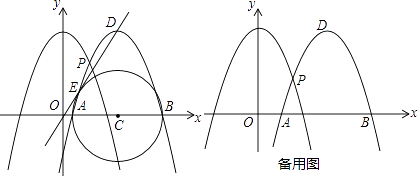

（1）直接写出抛物线解析式；
（2）如图，将抛物线向右平移k个单位，设平移后抛物线的顶点为D，与x轴的交点为A、B，与原抛物线的交点为P．
①当直线OD与以AB为直径的圆相切于E时，求此时k的值；
②是否存在这样的k值，使得点O、P、D三点恰好在同一条直线上？若存在，求出k值；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵抛物线的顶点为（0，4），

∴可设抛物线解析式为y=ax2+4，

又∵抛物线过点（2，0），

∴0=4a+4，解得a=﹣1，

∴抛物线解析式为y=﹣x2+4；

（2）

解：①如图，连接CE，CD．

∵OD是⊙C的切线，∴CE⊥OD．

在Rt△CDE中，∠CED=90°，CE=AC=2，DC=4，

∴∠EDC=30°，

∴在Rt△CDO中，∠OCD=90°，CD=4，∠ODC=30°，

∴OC= ，

∴当直线OD与以AB为直径的圆相切时，k=OC= ；

②存在k=2 ，能够使得点O、P、D三点恰好在同一条直线上．理由如下：

设抛物线y=﹣x2+4向右平移k个单位后的解析式是y=﹣（x﹣k）2+4，它与y=﹣x2+4交于点P，

由﹣（x﹣k）2+4=﹣x2+4，解得x1= ，x2=0（不合题意舍去），

当x= 时，y=﹣ k2+4，

∴点P的坐标是（ ，﹣ k2+4）．

设直线OD的解析式为y=mx，把D（k，4）代入，

得mk=4，解得m= ，

∴直线OD的解析式为y= x，

若点P（ ，﹣ k2+4）在直线y= x上，得﹣ k2+4= ，

解得k=±2 （负值舍去），

∴当k=2 时，O、P、D三点在同一条直线上．

【解析】（1）由抛物线的顶点为（0，4），可设抛物线解析式为y=ax2+4，再将点（2，0）代入，求出a=﹣1，即可得到抛物线解析式为y=﹣x2+4；（2）①连接CE，CD，先根据切线的性质得出CE⊥OD，再解Rt△CDE，得出∠EDC=30°，然后解Rt△CDO，得出OC= ，则k=OC= ；②设抛物线y=﹣x2+4向右平移k个单位后的解析式是y=﹣（x﹣k）2+4，它与y=﹣x2+4交于点P，先求出交点P的坐标是（ ，﹣ k2+4），再利用待定系数法求出直线OD的解析式为y= x，然后将点P的坐标代入y= x，即可求出k的值．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．