题目内容
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树形图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.
【答案】
(1)
解:如图所示:
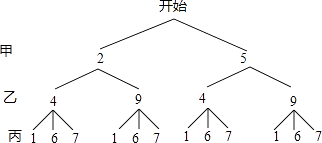 ,
,
所以共有12种可能出现的结果;
(2)
解:这些线段能够成三角形(记为事件A)的结果有4种:(5,4,6);(5,4,7);(5,9,6)(5,9,7),
所以P(A)= ![]() =
= ![]() .
.
【解析】(1)依据题意画树状图法分析所有等可能的出现结果即可解答;(2)根据树状图结合三角形的三边关系列举出能够成三角形的情况,用能够成三角形的情况数:总的情况数即可得到概率.

练习册系列答案
相关题目
【题目】瑶寨中学食堂为学生提供了四种价格的午餐供其选择,这四种价格分别是:A.3元,B.4元,C.5元,D.6元.为了了解学生对四种午餐的购买情况,学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况,依据统计数据制成如下的统计图表:
甲、乙两班学生购买午餐的情况统计表
品种 | A | B | C | D |
甲 | 6 | 22 | 16 | 6 |
乙 | ? | 13 | 25 | 3 |

(1)求乙班学生人数;
(2)求乙班购买午餐费用的中位数;
(3)已知甲、乙两班购买午餐费用的平均数为4.44元,从平均数和众数的角度解答,哪个班购买的午餐价格较高?
(4)从这次接受调查的学生中,随机抽查一人,恰好是购买C种午餐的学生的概率是多少?