题目内容
【题目】如图,正方形ABCD的边长为4厘米,动点P从点A出发沿AB边由A向B以1厘米/秒的速度匀速移动(点P不与点A、B重合),动点Q从点B出发沿拆线BC-CD以2厘米/秒的速度匀速移动。点P、Q同时出发,当点P停止运动,点Q也随之停止。联结AQ交BD于点E。设点P运动时间为t秒。
(1)用t表示线段PB的长;
(2)当点Q在线段BC上运动时,t为何值时,∠BEP和∠BEQ相等;
(3)当t为何值时,线段P、Q之间的距离为2![]() cm.
cm.

【答案】(1)PB=4-t;(2)t=![]() ;(3)t=2或
;(3)t=2或![]() ;
;
【解析】
(1)根据正方形的性质和已知条件即可求解;(2)由正方形的性质得出∠PBE=∠QBE,再证明△BEP≌△BEQ,根据全等三角形的性质可得BP=BQ,即可得出方程4-t=2t,解方程即可求得t值;(3)分两种情况讨论:①当![]() 时和②当
时和②当![]() 时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
时,根据已知条件,利用勾股定理得出方程,解方程即可求得t的值.
(1)PB=AB-AP,
∵AB=4,AP=1×t=t,
∴PB=4-t.
(2)当t=![]() 时,∠BEP和∠BEQ相等,理由如下:
时,∠BEP和∠BEQ相等,理由如下:
∵四边形ABCD正方形,
∴ 对角线BD平分∠ABC,
∴∠PBE=∠QBE,
当∠BEP=∠BEQ 时,
在△BEP和△BEQ中,
 ,
,
∴△BEP≌△BEQ,
∴BP=BQ,
即4-t=2t,
解得t=![]() ;
;
(3)分两种情况讨论:
①当![]() 时,即当P点在AB上,Q点在BC上运动时,
时,即当P点在AB上,Q点在BC上运动时,
连接PQ,如图1所示:

根据勾股定理得:![]() ,
,
即![]()
解得t=2或t=![]() (负值舍去);
(负值舍去);
②当![]() 时,即当P点在AB上,Q点在CD上运动时,
时,即当P点在AB上,Q点在CD上运动时,
作PM⊥CD于M,如图2所示:
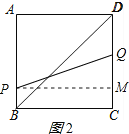
∴PM=BC=4,CM=BP=4-t,MQ=2t-4-(4-t)=3t-8,
根据勾股定理得:![]() ,
,
即![]()
解得t=2(舍去)或t=![]() ;
;
综上,当t=2或t=![]() 时,PQ之间的距离为2
时,PQ之间的距离为2![]() cm.
cm.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案




