Question

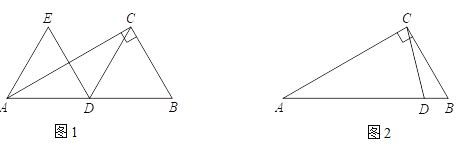
【题目】在△ABC中，∠ACB=90°，∠CAB=30°，点D在AB上，连接CD，并将CD绕点D逆时针旋转60°得到DE，连接AE．

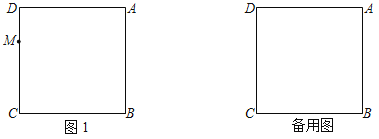
（1）如图1，当点D为AB中点时，直接写出DE与AE长度之间的数量关系；

（2）如图2，当点D在线段AB上时，

① 根据题意补全图2；

② 猜想DE与AE长度之间的数量关系，并证明．

Answer 1

【答案】（1）DE=AE；（2）①补全图形见解析；②DE=AE，证明见解析.

【解析】

（1）想办法证明△ADE是等边三角形即可解决问题．

（2）①根据要求画出图形即可．

②首先证明△的长，△FBC都是等边三角形，再证明△ECF≌△DCB，推出∠4＝∠5＝60°，证明△EFA≌△EFC（SAS）可得结论．

解：（1）结论：DE＝AE．

理由：如图1中，

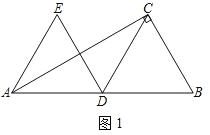
∵∠ACB＝90°，∠BAC＝30°，

∴AB＝2BC，∠B＝60°，

∵AD＝DB，

∴CD＝AD＝DB，

∴△CDB是等边三角形，

∴∠CDB＝60°，

∵DC＝DE，∠CDE＝60°，

∴∠ADE＝180°﹣∠ED﹣∠CDB＝60°，

∵DA＝DC，DC＝DE，

∴AD＝DE，

∴△ADE是等边三角形，

∴DE＝AE．

（2）①图形如图2所示：

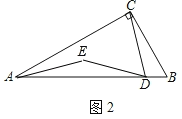
②如图2﹣1中，结论：DE＝AE．

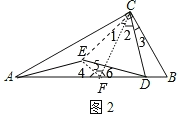
理由：取AB的中点F，连接CE，CF，EF．

∵∠ACB＝90°，AF＝BF，

∴CF＝AF＝BF，

∵∠B＝60°，

∴△BCF是等边三角形，

∵DC＝DE，∠CDE＝60°，

∴△ECD是等边三角形，

∴∠1+∠2＝∠2+∠3＝60°，CE＝CD，CF＝CB，

∴∠1＝∠3，

∴△ECF≌△DCB（SAS），

∴∠5＝∠B＝60°，

∵∠6＝60°，

∴∠4＝∠5＝60°，

∵EF＝EF，FA＝FC，

∴△EFA≌△EFC（SAS），

∴AE＝EC，

∵EC＝ED，

∴AE＝ED．