题目内容
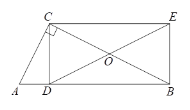
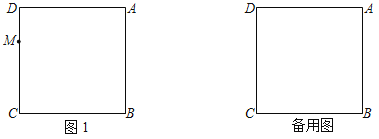
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
【答案】(1)详见解析;(2)![]() ;(3)1或
;(3)1或![]() .
.
【解析】
(1)根据题意作出图形便可,
(2)连接BM,先证明△ADM≌△ABF,再证明△FAE≌△MAB,求得BM,便可得EF;
(3)设DM=x(x>0),求出AE、AF、EF,当△AEF为等腰三角形,分两种情况:AE=EF或AF=EF,列出方程求出x的值,进而求得最后结果.
解:(1)根据题意作图如下:
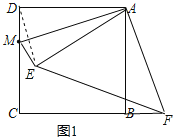
(2)连接BM,如图2,
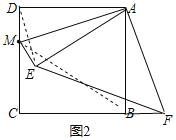
∵点D与点E关于AM所在直线对称,
∴AE=AD,∠MAD=∠MAE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°,
∵BM=BF,
∴△ADM≌△ABF(SAS),
∴AF=AM,∠FAB=∠MAD,
∴∠FAB=∠NAE,
∴∠FAE=∠MAB,
∴△FAE≌△MAB(SAS),
∴EF=BM,
∵四边形ABCD是正方形,
∴BC=CD=AB=3,
∵DM=1,
∴CM=2,
∴BM=![]() ,
,
∴EF=![]() ;
;
(3)设DM=x(x>0),则CM=3﹣x,
∴EF=BM=![]() ,
,
∵AE=AD=3,AF=AM=![]() ,
,
∴AF>AE,
∴当△AEF为等腰三角形时,只能有两种情况:AE=EF,或AF=EF,
①当AE=EF时,有![]() =3,解得x=3
=3,解得x=3
∴tan∠DAM=![]() ;
;
②当AF=EF时,![]() =
=![]() ,解得,x=
,解得,x=![]() ,
,
∴tan∠DAM=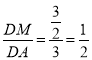 ,
,
综上,tan∠DAM的值为1或![]() .
.
故答案为:tan∠DAM的值为1或![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目