ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕ‘”ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–ΒΡ»Έ“β“ΜΒψ
÷–ΒΡ»Έ“β“ΜΒψ![]() Θ§Ηχ≥ω»γœ¬Ε®“εΘΚΨ≠ΙΐΒψ
Θ§Ηχ≥ω»γœ¬Ε®“εΘΚΨ≠ΙΐΒψ![]() «“ΤΫ––”ΎΝΫΉχ±ξ÷αΦ–Ϋ«ΤΫΖ÷œΏΒΡ÷±œΏΘ§Ϋ–ΉωΒψ
«“ΤΫ––”ΎΝΫΉχ±ξ÷αΦ–Ϋ«ΤΫΖ÷œΏΒΡ÷±œΏΘ§Ϋ–ΉωΒψ![]() ΒΡΓΑΧΊ’ςœΏΓ±Θ°άΐ»γΘΚΒψ
ΒΡΓΑΧΊ’ςœΏΓ±Θ°άΐ»γΘΚΒψ![]() ΒΡΧΊ’ςœΏ «
ΒΡΧΊ’ςœΏ «![]() ΚΆ
ΚΆ![]() Θ°
Θ°
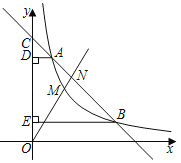
Θ®1Θ©»τΒψ![]() ΒΡΤδ÷–“ΜΧθΧΊ’ςœΏ «
ΒΡΤδ÷–“ΜΧθΧΊ’ςœΏ «![]() Θ§‘ρ‘Ύ
Θ§‘ρ‘Ύ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΗωΒψ÷–Θ§Ω…Ρή «Βψ
»ΐΗωΒψ÷–Θ§Ω…Ρή «Βψ![]() ΒΡΒψ”–_______ΘΜ
ΒΡΒψ”–_______ΘΜ
Θ®2Θ©“―÷ΣΒψ![]() ΒΡΤΫ––”ΎΒΎΕΰΓΔΥΡœσœόΦ–Ϋ«ΤΫΖ÷œΏΒΡΧΊ’ςœΏ”κ
ΒΡΤΫ––”ΎΒΎΕΰΓΔΥΡœσœόΦ–Ϋ«ΤΫΖ÷œΏΒΡΧΊ’ςœΏ”κ![]() ÷αœύΫΜ”ΎΒψ
÷αœύΫΜ”ΎΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§«“”κ
Θ§«“”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ° Ι
Θ° Ι![]() ΒΡΟφΜΐ≤Μ–Γ”Ύ6Θ§«σ
ΒΡΟφΜΐ≤Μ–Γ”Ύ6Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©“―÷ΣΒψ![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() ΒΡΑκΨΕΈΣ1Θ°Β±
ΒΡΑκΨΕΈΣ1Θ°Β±![]() ”κΒψ
”κΒψ![]() ΒΡΧΊ’ςœΏ¥φ‘ΎΫΜΒψ ±Θ§÷±Ϋ”–¥≥ω
ΒΡΧΊ’ςœΏ¥φ‘ΎΫΜΒψ ±Θ§÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() «“
«“![]() Θ®Μρ’ΏΘΚ
Θ®Μρ’ΏΘΚ![]() «“
«“![]() Θ©ΘΜΘ®3Θ©
Θ©ΘΜΘ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Μ≠≥ωΆΦ–ΈΘ§ΗυΨίΒψΒΡΧΊ’ςœΏΒΡΕ®“εΫβΨωΈ ΧβΦ¥Ω…Θ°
Θ®2Θ©ΙΐΒψPΤΫ––”ΎΒΎΕΰΥΡœσœόΫ«ΤΫΖ÷œΏΒΡΧΊ’ςœΏΒΡΫβΈω ΫΈΣy=-x+bΘ§«σ≥ωΓςPABΒΡΟφΜΐΈΣ6 ±ΒψBΒΡΉχ±ξΘ§‘Όάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ÷±œΏPBΒΡΫβΈω ΫΘ§ΫαΚœΆΦ–ΈΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®3Θ©»γΆΦ3÷–Θ§”…Χβ“βΒψCΒΡΧΊ’ςœΏΒΡΫβΈω ΫΈΣy=x-2Μρy=-x+2Θ§…ηΒ±Γ―T”κ÷±œΏy=-x+2œύ«–”ΎΒψM ±Θ§Β±Γ―TΓδ”κ÷±œΏy=x-2œύ«–”ΎΒψN ±Θ§Ζ÷±π«σ≥ωOTΘ§OTΓδΫαΚœΆΦœσΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©»γΆΦ1÷–Θ§Ιέ≤λΆΦœσΩ…÷ΣΘ§ΒψD2ΒΡΧΊ’ςœΏ «y=x+1Θ°

Ι ¥πΑΗΈΣD2Θ°
Θ®2Θ©»γΆΦ2÷–Θ§

…ηΙΐΒψPΤΫ––”ΎΒΎΕΰΥΡœσœόΫ«ΤΫΖ÷œΏΒΡΧΊ’ςœΏΒΡΫβΈω ΫΈΣy=-x+bΘ§
Γύ1+b=2Θ§
Γύb=1Θ§
ΓύΙΐΒψPΤΫ––”ΎΒΎΕΰΥΡœσœόΫ«ΤΫΖ÷œΏΒΡΧΊ’ςœΏΒΡΫβΈω ΫΈΣy=-x+1Θ§
ΓύAΘ®1Θ§0Θ©Θ§
Β±ΓςBPAΒΡΟφΜΐ=6 ±Θ§![]() ABΓΝ2=6Θ§
ABΓΝ2=6Θ§
ΓύAB=6Θ§
ΓύBΘ®-5Θ§0Θ©ΜρΘ®7Θ§0Θ©Θ§
Β±y=kx+bΓδΨ≠ΙΐPΘ®-1Θ§2Θ©Θ§BΘ®-5Θ§0Θ© ±Θ§
![]() ΫβΒΟk=
ΫβΒΟk=![]() Θ§
Θ§
Β±÷±œΏy=kx+bΓδΨ≠ΙΐPΘ®-1Θ§2Θ©Θ§BΘ®7Θ§0Θ© ±Θ§
![]() Θ§ΫβΒΟk=-
Θ§ΫβΒΟk=-![]() Θ§
Θ§
Ιέ≤λΆΦ–ΈΩ…÷Σ¬ζΉψΧθΦΰΒΡkΒΡ÷ΒΈΣ-![]() ΓήkΓή
ΓήkΓή![]() «“kΓΌ0Θ°
«“kΓΌ0Θ°
Θ®3Θ©»γΆΦ3÷–Θ§”…Χβ“βΒψCΒΡΧΊ’ςœΏΒΡΫβΈω ΫΈΣy=x-2Μρy=-x+2Θ§

Β±Γ―T”κ÷±œΏy=-x+2œύ«–”ΎΒψM ±Θ§Ν§Ϋ”TMΘ§
‘ΎRtΓςTCM÷–Θ§ΓΏΓœTMC=90ΓψΘ§ΓœMCT=45ΓψΘ§
ΓύMT=MC=1Θ§
ΓύTC=![]() TM=
TM=![]() Θ§
Θ§
ΓύOT=2-![]() Θ§¥Υ ±t=2-
Θ§¥Υ ±t=2-![]() Θ°
Θ°
Β±Γ―TΓδ”κ÷±œΏy=x-2œύ«–”ΎΒψN ±Θ§ΆΤ≥ωΖ®Ω…ΒΟOTΓδ=2+![]() Θ§¥Υ ±t=2+
Θ§¥Υ ±t=2+![]() Θ§
Θ§
ΫαΚœΆΦœσΩ…÷Σ¬ζΉψΧθΦΰΒΡtΒΡ÷ΒΈΣΘΚ2-![]() ΓήΓή2+
ΓήΓή2+![]() Θ°
Θ°

 Ή÷¥ ΨδΕΈΤΣœΒΝ–¥πΑΗ
Ή÷¥ ΨδΕΈΤΣœΒΝ–¥πΑΗ