题目内容
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
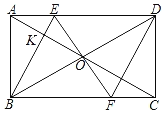
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
【答案】(1)见解析;(2)32
【解析】
(1)四边形ABCD是平行四边形,可以证明△DEO≌△BFO,可得OE=OF,从而四边形EBFD是平行四边形,根据EF⊥BD,进而可得平行四边形EBFD是菱形;
(2)证明△AEK∽△CBK,对应边成比例可得BC=12,进而求出DE的长,可得菱形的周长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠EDO=∠FBO,
OB=OD,
∠EOF=∠FOB,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴平行四边形EBFD是菱形;
(2)∵AE//BC,
∴△AEK∽△CBK,
∴![]() =
=![]() ,
,
∵BK=3EK,AE=4,
∴![]() =
=![]() ,
,
∴BC=12,
∴AD=BC=DE+AE=DE+4=12,
∴DE=8,
∴菱形EBFD的周长为4DE=32.
答:四边形EBFD的周长为32.

练习册系列答案
相关题目