Question

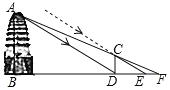
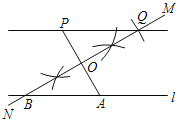
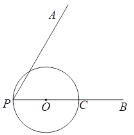
【题目】如图，∠APB，点C在射线PB上，PC为⊙O的直径，在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M，图形M交⊙O于D，过点D作直线DE⊥PA，分别交射线PA，PB于E，F．

（1）根据题意补全图形；

（2）求证：DE是⊙O的切线；

（3）如果PC=2CF，且，求PE的长．

Answer 1

【答案】（1）作图见解析；（2）证明见解析；（3）．

【解析】

（1）根据题目要求画出图形即可得到．
（2）连接OD，利用角平分线的性质以及平行的性质证明DE⊥OD，即可证明DE是⊙O的切线．
（3）先证明OF=2OD，推出∠OFD=30°，解直角三角形求出OD，OF，PF即可解决问题．

解：（1）如图所示，补全图形

（2）证明：连接OD．

∵DE⊥PA，

∴∠PED=90°．

∵依题意，PD是∠APB的角平分线，

∴∠APD=∠DPB．

∵OP=OD，

∴∠DPB =∠PDO．

∴∠APD=∠PDO．

∴AP∥OD，

∴∠ODF=∠PED=90°，

∴DE是⊙O的切线．

（3）∵PC=2CF，

∴设CF=x，那么PC=2x，OD=x．

∵∠ODF=90°，

∴在Rt△ODF中，OD=．

又∵ ，

∴OD=1，OF=2，PF=3．

∵在Rt△PEF中，∠PEF=90°，

∴．

∴．