题目内容
【题目】如图,已知△ABC,
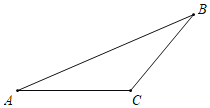
(1)按如下步骤尺规作图(保留作图痕迹):
①作AD平分∠BAC,交BC于D;
②作AD的垂直平分线MN分别交AB,AC于点E、F;
(2)连接DE、DF.若BD=12,AF=8,CD=6,求BE的长.
【答案】(1)如图,AD和EF为所作;见解析;(2)BE=16.
【解析】
(1)①根据尺规作角平分线的方法作图即可;②根据尺规作线段垂直平分线的方法作图即可;
(2)先证明四边形AEDF为菱形,得AE=AF=8,DE∥AC,再根据平行线分线段成比例定理即可求得结果.
解:(1)如图,AD和EF为所作;

(2)∵EF垂直平分AD,
∴EA=ED,FA=FD,AD⊥EF,
∵AD平分∠EAF,
∴AD平分EF,
即AD和EF互相垂直平分,
∴四边形AEDF为菱形,
∴AE=AF=8,DE∥AC,
∴![]() ,即
,即![]() ,
,
∴BE=16.

练习册系列答案
相关题目
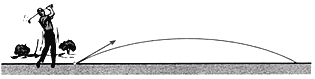
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.