题目内容
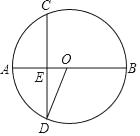
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接OD.
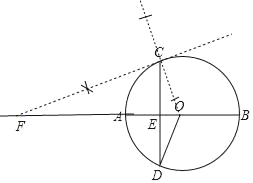
(1)过点C作射线CF交BA的延长线于点F,且使得∠ECF=∠AOD;(要求尺规作图,不写作法)
(2)求证:CF是⊙O的切线;
(3)若OE:AE=1:2,且AF=6,求⊙O的半径.
【答案】(1)见解析(2)证明见解析(3)3
【解析】
(1)连接OC,根据尺规作图方法,作∠ECF=∠AOD,交BA的延长线于点F即可.
(2)通过证明∠OCF=90°即可.
(3),由OE:AE=1:2可知OA=3AE,由△OCE∽△OFC可知OF=3OC,可求出OE的长度进而求出OA即可.
(1)解:如图直线CF即为所求;
(2)∵OC=OD
∴∠OCE=∠ODE
∵CD⊥AB
∴∠DOE+∠ODE=90°
∵∠ECF=∠AOD,∠OCE=∠ODE
∴∠OCE+∠ECF=90°,即∠OCF=90°,
∴直线CF是⊙O的切线.
(3)解:设OE=a,则AE=2a,OC=OA=3a.
∵△OCE∽△OFC,
∴![]()
∴OF=3OC,
∴6+3a=9a,
∴a=1,
∴OC=3.

练习册系列答案
相关题目