题目内容
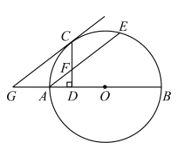
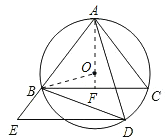
【题目】如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD。

(1)求证:∠ADB=∠E;
(2)当AB=5,BC=6时,求⊙O的半径.
【答案】(1)见解析;(2)![]()
【解析】
(1)由AB=AC,可证∠ABC=∠C;由平行线的性质知∠ABC=∠E,结合圆周角定理可证结论成立;
(2)可通过构建直角三角形来求解,连接BO、AO,并延长AO交BC于点F,根据垂径定理BF=CF,AF=r+OF,那么直角三角形OBF中可以用R表示出OF,OB,然后根据勾股定理求出半径的长.
解:(1)在△ABC中,
∵AB=AC,
∴∠ABC=∠C.
∵DE∥BC,
∴∠ABC=∠E,
∴∠E=∠C.
又∵∠ADB=∠C,
∴∠ADB=∠E;
(2)连线BO、AO,并延长AO交BC于点F,则AF⊥BC,且BF=CF=3,
又∵AB=5,
∴AF=![]() =4。
=4。
设⊙O的半径为r,在Rt△OBF中,OF=4-r,OB=r,BF=3,
∴r2=32+(4-r)2,
解得r=![]() ,
,
∴⊙O的半径是![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目