题目内容
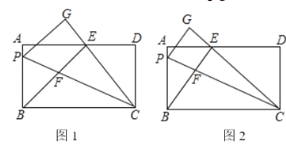
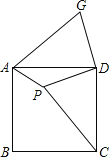
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )
A.150°B.135°C.120°D.108°
【答案】B
【解析】
连接PG,由题意得出PD=GD=2,∠CDP=∠ADG,得出∠PDG=∠ADC=90°,得出△PDG是等腰直角三角形,由等腰直角三角形的性质得出∠GPD=45°,PG=![]() PD=2
PD=2![]() ,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
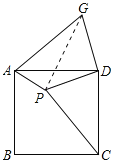
解:连接PG,如图所示:
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,AG=PC=3,
∵PA=1,PD=2,PC=3,将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),
∴PD=GD=2,∠CDP=∠ADG,
∴∠PDG=∠ADC=90°,
∴△PDG是等腰直角三角形,
∴∠GPD=45°,PG=![]() PD=2
PD=2![]() ,
,
∵AG=PC=3,AP=1,PG=2![]() ,
,
∴AP2+PG2=AG2,
∴∠GPA=90°,
∴∠APD=90°+45°=135°;
故选:B.

练习册系列答案
相关题目