题目内容
【题目】材料:帕普斯借助函数给出了一种“三等分锐角”的方法,具体如下:
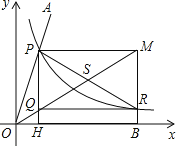
①建立平面直角坐标系,将已知锐角∠AOB的顶点与原点O重合,角的一边OB与x轴正方向重合;
②在平面直角坐标系里,绘制函数y=![]() 的图象,图象与已知角的另一边OA交于点P;
的图象,图象与已知角的另一边OA交于点P;
③以P为圆心,2OP为半径作弧,交函数y=![]() 的图象于点R;
的图象于点R;
④分别过点P和R作x轴和y轴的平行线,两线相交于点M、Q;
⑤连接OM,得到∠MOB,这时∠MOB=![]() ∠AOB.
∠AOB.
根据以上材料解答下列问题:
(1)设点P的坐标为(a,![]() ),点R的坐标为(b,
),点R的坐标为(b,![]() ),则点M的坐标为 ;
),则点M的坐标为 ;
(2)求证:点Q在直线OM上;
(3)求证:∠MOB=![]() ∠AOB;
∠AOB;
(4)应用上述方法得到的结论,如何三等分一个钝角(用文字简要说明).
【答案】(1)(b,![]() );(2)见详解;(3)见详解;(4)见详解.
);(2)见详解;(3)见详解;(4)见详解.
【解析】
(1)根据点P和点R的坐标,直接求出点M的坐标,即可;
(2)先用待定系数法,求出直线OM的解析式,再求出点Q的坐标,进而即可得到结论;
(3)根据矩形的性质,得∠SQR=∠SRQ,由作图过程中的条件,得PS=OP,由三角形外角的性质定理,结合点Q在直线OM上,可得∠PSO=2∠SQR,进而即可得证;
(4)既然能作出锐角的三等分角,先将钝角的一半(锐角)三等分,再作钝角的三等分角,即可.
(1)∵点P的坐标为(a,![]() ),点R的坐标为(b,
),点R的坐标为(b,![]() ),分别过点P和R作x轴和y轴的平行线,两线相交于点M、Q,
),分别过点P和R作x轴和y轴的平行线,两线相交于点M、Q,
∴M(b,![]() ).
).
故答案是:(b,![]() );
);
(2)设直线OM的解析式为:y=kx,
把M(b,![]() )代入y=kx,得
)代入y=kx,得![]() =kb,解得:k=
=kb,解得:k=![]() ,
,
∴y=![]() x,
x,
由第(1)小题,可知:Q(a,![]() ),
),
∴![]() =
=![]() a成立,
a成立,
∴点Q在直线OM上;
(3)∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=![]() PR,
PR,
∴∠SQR=∠SRQ,
∵PR=2OP,
∴PS=OP=![]() PR,
PR,
∴∠POS=∠PSO,
∵点Q在直线OM上,∠PSQ是△SQR的一个外角,
∴∠PSO=2∠SQR,
∴∠POS=2∠SQR,
∵QR∥OB,
∴∠MOB=∠SQR,
∴∠POS=2∠MOB,
∴∠MOB=![]() ∠AOB;
∠AOB;
(4)先作出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,再作一个角与已作得的角相等,进而即可得到钝角的三等分角.

【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.