题目内容
【题目】函数y=mx+n与
，其中m≠0，n≠0，那么它们在同一坐标系中的图象可能是（ ）
A．
B．
C．
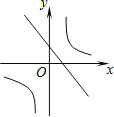D．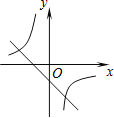
【答案】B．
【解析】
试题根据图象中一次函数图象的位置确定m、n的值；然后根据m、n的值来确定反比例函数所在的象限，对各选项作出判断：
A、∵函数y=mx+n经过第一、三、四象限，∴m＞0，n＜0．
∴
＜0．∴函数y=
的图象经过第二、四象限．与图示图象不符．故本选项错误．
B、∵函数y=mx+n经过第一、三、四象限，∴m＞0，n＜0．
∴＜0．∴函数的y=图象经过第二、四象限．与图示图象一致．故本选项正确．
C、∵函数y=mx+n经过第一、二、四象限，∴m＜0，n＞0．
∴＜0．∴函数的y=图象经过第二、四象限．与图示图象不符．故本选项错误．
D、∵函数y=mx+n经过第二、三、四象限，∴m＜0，n＜0．
∴＞0． ∴函数的y=图象经过第一、三象限．与图示图象不符．故本选项错误．
故选B．
练习册系列答案
相关题目
