Question

【题目】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=900，点A、C的坐标分别为A(-2,0),C(1,0),tan∠BAC=.

（1）求点B的坐标。

（2）在x轴上找一点D，连接DB，使得△BCD与△ABC相似（不包括全等），并求点D的坐标。

Answer 1

【答案】（1）B（1，2）（2）D(,0),(- ,0)

【解析】试题分析：(1)由点A、C坐标得出AC的长度，在直角△ABC，根据tan∠BAC=，求得BC的长度，即可得出点B的坐标；

（2）分情况讨论：①当点D在点C右边时，根据相似三角形的性质求得CD的长，即可得出点D的坐标；①当点D在点C左边时，根据相似三角形的性质求得CD的长，即可得出点D的坐标；

试题解析：

∵A(-2,0),C(1,0),

∴AC=3,

又∵△ABC是直角三角形, tan∠BAC=,

∴ ，

∴BC＝2，

∴点B的坐标为（1，2）.

（2）①当点D在点C右边时，如图所示

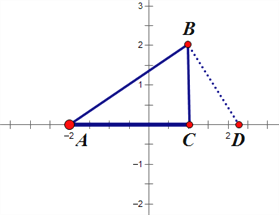
∵使得△BCD与△ABC相似，

∴ ，

∴CD＝ ，

∴点D的坐标为（1+，0），即(,0);

②当点D在点C左边时，如图所示

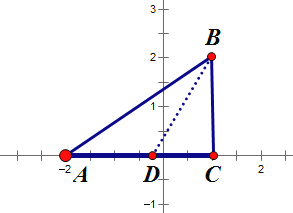
∵使得△BCD与△ABC相似，

∴ ，

∴CD＝ ，

∴点D的坐标为（1－，0），即(-,0);

综合上述可得：点D的坐标(,0)或(-,0).