题目内容
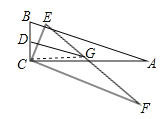
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC=6![]() ,BC的中点为D,将△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,连接DG在旋转过程中,DG的最大值是_______.
,BC的中点为D,将△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,连接DG在旋转过程中,DG的最大值是_______.

【答案】9
【解析】
解直角三角形求出AB、BC,再求出CD,连接CG,根据直角三角形斜边上的中线等于斜边的一半求出CG,然后根据三角形的任意两边之和大于第三边判断出D、C、G三点共线时DG有最大值,再代入数据进行计算即可得解.
∵∠ACB=90°,∠A=30°,
∴AB=AC÷cos30°=![]() ,
,
BC=ACtan30°=![]() ,
,
∵BC的中点为D,
∴CD=![]() BC=
BC=![]() ×6=3,
×6=3,
连接CG,
∵△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,
∴CG=![]() EF=
EF=![]() AB=
AB=![]() ×12=6,
×12=6,
由三角形的三边关系得,CD+CG>DG,
∴D、C、G三点共线时DG有最大值,
此时DG=CD+CG=3+6=9.
故答案为:9

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】经测算,某地气温![]() 与距离地面的高度
与距离地面的高度![]() 有如下对应关系:
有如下对应关系:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表,完成下面的问题.
(1)猜想:距离地面的高度每上升![]() ,气温就下降______
,气温就下降______![]() ;表中
;表中![]() ______.
______.
(2)气温![]() 与高度
与高度![]() 之间的函数关系式是______.
之间的函数关系式是______.
(3)求该地距离地面![]() 处的气温.
处的气温.